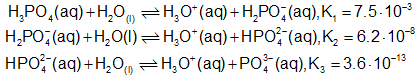Question: The pH of normal urine is 6.30, and the total phosphate concentration \(\left( {\left( {PO_4^{3 - }} \right) + \left( {HPO_4^{2 - }} \right) + \left( {{H_2}PO_4^ - } \right)} \right.\)\(\left. { + \left( {{H_3}P{O_4}} \right)} \right)\)is 0.020 M. What is the minimum concentration of \(C{a^{2 + }}\) necessary to induce kidney stone formation? (See Exercise 15.49 for additional information.)

Let’s consider, \(\left( {{{\rm{H}}^ + }} \right)\) in the urine to be able to predict dissociation of other ions.

\(\begin{array}{*{20}{c}}{{\rm{pH}} = - \log \left( {{{\rm{H}}^ + }} \right)}\\{6.3 = - \log \left( {{{\rm{H}}^ + }} \right)}\\{\log \left( {{{\rm{H}}^ + }} \right) = - 6.3}\end{array}\)

\(\begin{array}{*{20}{c}}{\left( {{{\rm{H}}^ + }} \right) = {\rm{antilog\;}}( - 6.3)}\\{\left( {{{\rm{H}}^ + }} \right) = 5.01 \cdot {{10}^{ - 7}}}\end{array}\)

Dissociation of Phosphate,

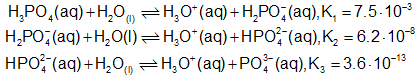
\({{\rm{K}}_3} = \frac{{\left( {{{\rm{H}}_3}{{\rm{O}}^ + }} \right)\left( {{\rm{PO}}_4^{3 - }} \right)}}{{\left( {{\rm{HPO}}_4^{2 - }} \right)}}\)

\(\begin{array}{*{20}{c}}{3.6 \cdot {{10}^{ - 13}} = \frac{{5.01 \cdot {{10}^{ - 7}}\left( {{\rm{PO}}_4^{3 - }} \right)}}{{\left( {{\rm{HPO}}_4^{2 - }} \right)}}}\\{\left( {{\rm{HPO}}_4^{2 - }} \right) = \frac{{5.01 \cdot {{10}^{ - 7}}}}{{3.6 \cdot {{10}^{ - 13}}}}\left( {{\rm{PO}}_4^{3 - }} \right)}\end{array}\)

\(\left( {{\rm{HPO}}_4^{2 - }} \right) = 1.39 \cdot {10^6}\left( {{\rm{PO}}_4^{3 - }} \right)\)

So, the concentration is expressed as \(\left( {{\rm{PO}}_4^{3 - }} \right){\rm{\;is\;}}1.39 \cdot {10^6}\left( {{\rm{PO}}_4^{3 - }} \right)\).

\({{\rm{K}}_2} = \frac{{\left( {{{\rm{H}}_3}{{\rm{O}}^ + }} \right)\left( {{\rm{HPO}}_4^{2 - }} \right)}}{{\left( {{{\rm{H}}_2}{\rm{PO}}_4^ - } \right)}}\)

Substitute \(\left( {{\rm{PO}}_4^{3 - }} \right){\rm{\;is\;}}1.39 \cdot {10^6}\left( {{\rm{PO}}_4^{3 - }} \right)\)as we get in before step,

\(\begin{array}{*{20}{c}}{6.2 \cdot {{100}^8} = \frac{{5.01 \cdot {{10}^{ - 7}} \cdot 1.39 \cdot {{10}^6}\left( {{\rm{PO}}_1^{i - }} \right)}}{{\left( {{\rm{I}}{{\rm{I}}_2}{\rm{PO}}_4^ - } \right)}}}\\{\left| {{{\rm{H}}_2}{\rm{PO}}_4^ - } \right| = \frac{{0.696}}{{6.2 \cdot {{10}^{ - 8}}}}\left( {{\rm{P}}_4^{3 - }} \right)}\end{array}\)

\(\left( {{{\rm{H}}_2}{\rm{PO}}_4^ - } \right) = 1.12 \cdot {10^7}\left( {{\rm{PO}}_4^{3 - }} \right)\)

So, the concentration is expressed as \(\left( {{\rm{PO}}_4^{3 - }} \right){\rm{\;is\;}}1.12 \cdot {10^7}\left( {{\rm{PO}}_4^{3 - }} \right)\)

\({{\rm{K}}_1} = \frac{{\left( {{{\rm{H}}_3}{{\rm{O}}^ + }} \right)\left( {{{\rm{H}}_2}{\rm{PO}}_4^ - } \right)}}{{\left( {{{\rm{H}}_3}{\rm{P}}{{\rm{O}}_4}} \right)}}\)

Substitute\(\left( {{\rm{PO}}_4^{3 - }} \right){\rm{\;is\;}}1.12 \cdot {10^7}\left( {{\rm{PO}}_4^{3 - }} \right)\) as we get in before step,

\(\begin{array}{*{20}{c}}{7.5 \cdot {{10}^{ - 3}} = \frac{{5.01 \cdot {{10}^{ - 7}} \cdot 1.12 \cdot {{10}^7}\left( {{\rm{PO}}_4^{3 - }} \right)}}{{\left( {{{\rm{H}}_3}{\rm{P}}{{\rm{O}}_4}} \right)}}}\\{\left( {{{\rm{H}}_3}{\rm{P}}{{\rm{O}}_4}} \right) = \frac{{5.611}}{{7.5 \cdot {{10}^{ - 3}}}}\left( {{\rm{PO}}_4^{3 - }} \right)}\end{array}\)

\(\left( {{{\rm{H}}_3}{\rm{P}}{{\rm{O}}_4}} \right) = 748\left( {{\rm{PO}}_4^{3 - }} \right)\)

So, the concentration is expressed as \(\left( {{\rm{PO}}_4^{3 - }} \right){\rm{\;is\;}}748\left( {{\rm{PO}}_4^{3 - }} \right)\)

Phosphate concentration in urine is \(0.02{\rm{M}}\)

\(0.02 = \left( {{{\rm{H}}_3}{\rm{P}}{{\rm{O}}_4}} \right) + \left( {{{\rm{H}}_2}{\rm{PO}}_4^ - } \right) + \left( {{\rm{HPO}}_4^{2 - }} \right) + \left( {{\rm{PO}}_4^{3 - }} \right)\)

\(\begin{array}{*{20}{c}}{0.02 = 748 \setminus \left( {{\rm{PO}}_4^{3 - }} \right) + 1.12 \cdot {{10}^7}\left( {{\rm{PO}}_4^{3 - }} \right) + 1.39 \cdot {{10}^6}\left( {{\rm{PO}}_4^{3 - }} \right)}\\{0.02 = \left( {748 + 1.12 \cdot {{10}^7} + 1.39 \cdot {{10}^6}} \right)\left( {{\rm{PO}}_4^{3 - }} \right)}\end{array}\)

\(\begin{array}{*{20}{c}}{\left( {{\rm{PO}}_4^{3 - }} \right) = \frac{{0.02}}{{1.26 \cdot {{10}^7}}}}\\{\left( {{\rm{PO}}_4^{3 - }} \right) = 1.59 \cdot {{10}^{ - 9}}}\end{array}\)

As given \({{\rm{K}}_{sp}} = 1.3 \cdot {10^{ - 32}}\),

\(\begin{array}{*{20}{c}}{{{\left( {{\rm{C}}{{\rm{a}}^{2 + }}} \right)}^3} = \frac{{1.3 \cdot {{10}^{ - 32}}}}{{{{\left( {1.59 \cdot {{10}^{ - 9}}} \right)}^2}}}}\\{{{\left( {{\rm{C}}{{\rm{a}}^{2 + }}} \right)}^3} = 5.14 \cdot {{10}^{ - 15}}}\end{array}\)

\(\begin{array}{*{20}{c}}{\left( {{\rm{C}}{{\rm{a}}^{2 + }}} \right) = \sqrt(3){{5.14 \cdot {{10}^{ - 15}}}}}\\{\left( {{\rm{C}}{{\rm{a}}^{2 + }}} \right) = 1.73 \cdot {{10}^{ - 5}}{\rm{M}}}\end{array}\)

The minimum concentration of \({\rm{C}}{{\rm{a}}^{2 + }}\)that will trigger formation of kidney stones is \(1.73 \cdot {10^{ - 5}}{\rm{M}}\).