Let T be an MST of graph G. Given a connected subgraph H of G, show that $\mathbf{T}\mathbf{\cap }\mathbf{H}$ is contained in some MST of H

When explore together all nodes of a graph, a minimal spanning tree travels the all edges which do not create a cycle. Together all edges of T that do not make a cycle in T are included in an MST T of a graph G. A cycle may not even exist in a G sub-graph.

• Whenever H has a cycle, there would be a lot of MST of H. For each MST of H , an unique smallest node will be excluded. Once there is n nodes within and H and k cycles in H, there can be n-k edges in $\mathrm{T}\cap \mathrm{H}$because T visits all nodes in T that do not form a cycle.

• Because T has no cycle, the intersecting of H plus T will not have a cycle, omitting just those nodes of H that contribute to the creation of a cycle. As per definition of H, $\mathrm{T}\cap \mathrm{H}$ is an as it is containing all edges except the edge which is creating cycle. When $\mathrm{T}\cap \mathrm{H}$is itself an MST, then it is obvious that it is contained in itself.

Hence, it is proved that if H contains a cycle, then $\mathrm{T}\cap \mathrm{H}$ is contained in some MST of H.

• H is indeed an MST when it does not include a cycle. T is now an MST, thus, $\mathrm{T}\cap \mathrm{H}$ would then include all of H's nodes., $\mathrm{T}\cap \mathrm{H}=\mathrm{H}$. Whenever T & H both are equal to each other then $\mathrm{T}\cap \mathrm{H}$is also an MST.

• Whenever $\mathrm{T}\cap \mathrm{H}$ is MST, Then it would be evident that it's self-contained.

As a result, it can be demonstrated that if H does not include a cycle, then $\mathrm{T}\cap \mathrm{H}$ is contained in some MST of H.

$\mathrm{T}\cap \mathrm{H}$is H. occurs in some MST The evidence is demonstrated in the next section. Assume the graph G in Figure 1 is correct.

Figure 1

The MST of the graph will be as shown in Figure 2.

Figure 2

Figure 3 is a subgraph H of graph G .

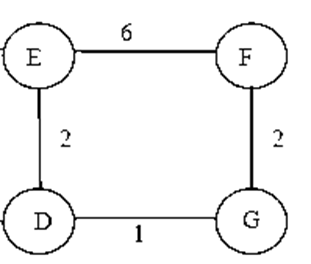
Figure 3

The MST of this graph will be as shown in Figure 4.

Figure 4

$\mathrm{T}\cap \mathrm{H}\mathrm{T}$ with H's shared edges will be contained. Figure 4 is role="math" localid="1658914214466" $\mathrm{T}\cap \mathrm{H}$. Thus, $\mathrm{T}\cap \mathrm{H}=\mathrm{MST}\left(H\right)$.If somehow the weight for ED in Figure 1 was 6, then the weight of ED in Figure 2 would be 6. But there would have been two MST of H, one with the ED edge and the other with the EF edge. However, there'd have been two MST of G as well. In either scenario, every MST of H would contain the crossover of any T with H.

As a result, is always present in some H MST.