A vertex cover of a graph $\mathbf{G}\mathbf{=}\left(V,E\right)\mathbf{}$is a subset of vertices $\mathbf{S}\mathbf{\subseteq }\mathbf{V}$that includes at least one endpoint of every edge in E. Give a linear-time algorithm for the following task.

Input: An undirected tree $\mathbf{T}\mathbf{=}\left(V,E\right)\mathbf{}$.

Output: The size of the smallest vertex cover of T. For instance, in the following tree, possible vertex covers include$\left\{A,B,C,D,E,F,G\right\}$and$\left\{A,C,D,F\right\}$but not$\left\{C,E,F\right\}\mathbf{.}$The smallest vertex cover has size 3: $\left\{B,E,G\right\}\mathbf{.}$

We have given a graph$\mathrm{G}=\left(\mathrm{V},\mathrm{E}\right)$ where we have to find the smallest vertex cover. Vertex cover is a set of vertices that includes at least one endpoint of every edge of the graph. In order to find the size of smallest vertex cover of the given graph, we will use dynamic programming approach where we will find out all possible vertex cover of all subproblems and then select that vertex cover which is smallest.

$\mathrm{v}\left(\mathrm{i}\right)=\min \left\{\sum _{\mathrm{j}:\mathrm{j}\in \mathrm{Child}\left(\mathrm{i}\right)}\left(1+\sum _{\mathrm{k}:\mathrm{k}\in \mathrm{Child}\left(\mathrm{j}\right)}\left(\mathrm{v}\left(\mathrm{k}\right)\right)\right),1+\sum _{\mathrm{j}:\mathrm{j}\in \mathrm{Child}\left(\mathrm{i}\right)}\mathrm{v}\left(\mathrm{j}\right)\right\}$

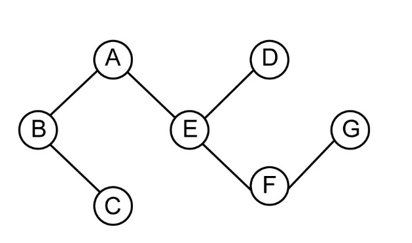
Let us suppose that for each node ‘$\left(u\right)$’ in the graph, we consider$\mathrm{V}\left(\mathrm{u}\right)$as the size of minimum vertex cover for a subtree which is rooted at node ‘$\left(u\right)$’.

Fig: A undirected graph.

Vertex cover is a set of vertices that includes at least one endpoint of every edge of the graph. In order to find the size of smallest vertex cover of the given graph, we will use dynamic programming approach where we will find out all possible vertex cover of all subproblems and then select that vertex cover which is smallest.

Our base condition will be when our node ‘u’ is leaf node. In this case, $V\left(u\right)=0$. This is because we cannot obtain subtree from leaf node.

For any internal node of a subtree, we have:

$\mathrm{v}\left(\mathrm{i}\right)=\min \left\{\sum _{\mathrm{j}:\mathrm{j}\in \mathrm{Child}\left(\mathrm{i}\right)}\left(1+\sum _{\mathrm{k}:\mathrm{k}\in \mathrm{Child}\left(\mathrm{j}\right)}\left(\mathrm{v}\left(\mathrm{k}\right)\right)\right),1+\sum _{\mathrm{j}:\mathrm{j}\in \mathrm{Child}\left(\mathrm{i}\right)}\mathrm{v}\left(\mathrm{j}\right)\right\}$

On solving the above recursive equation, we will get output as $\mathrm{V}\left(\mathrm{r}\right)$, where r is the root of the tree. Thus,$V\left(r\right)$is the size of the minimum vertex cover. The algorithm according to the above stated recursion relation, solve all the subproblem in order of decreasing depth of the tree.

This recursion will run in linear time that is $O\left(n\right).$