Let F be the language of all strings over $\left\{0,1\right\}$that do not contain a pair of 1s that are separated by an odd number of symbols. Give the state diagram of a DFA with five states that recognizes $F$ . (You may find it helpful first to find a 4-state NFA for the complement of $F$).

Consider the language $F$that contains the strings over $\left\{0,1\right\}$ , that does not contain a pair of 1s that are separated by an odd number of symbols.

The DFA is the Deterministic Finite Automata, which has deterministic states that have knowledge of the future of the transition.

Construct the NFA for the given statement, then convert it into a DFA. Construct the NFA, $F\text{'}$that it accepts the strings that do not contain a pair of 1s that are separated by an odd number of symbols.

The NFA, $F\text{'}$is as follows:

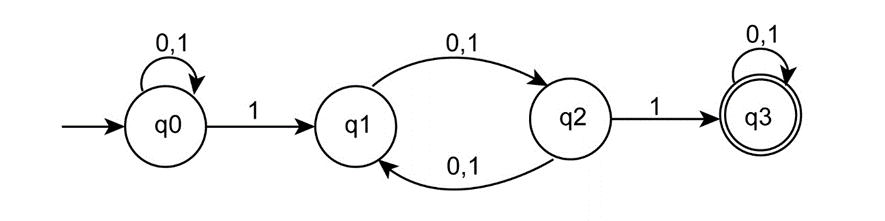
Convert the NFA to DFA as follows:

1. Create an empty set.
2. Make the initial state of NFA the same as the initial state of DFA and add the set of states of DFA.
3. Find the possible set of states for every new state for each input symbol by the transition function of NFA and add new states to the set of states.
4. Start the above transition from the initial state.
5. Stop the procedure if no new states are formed.
6. Declare the final states of DFA, which is the set of final states of NFA.

The state diagram of the DFA is as follows,

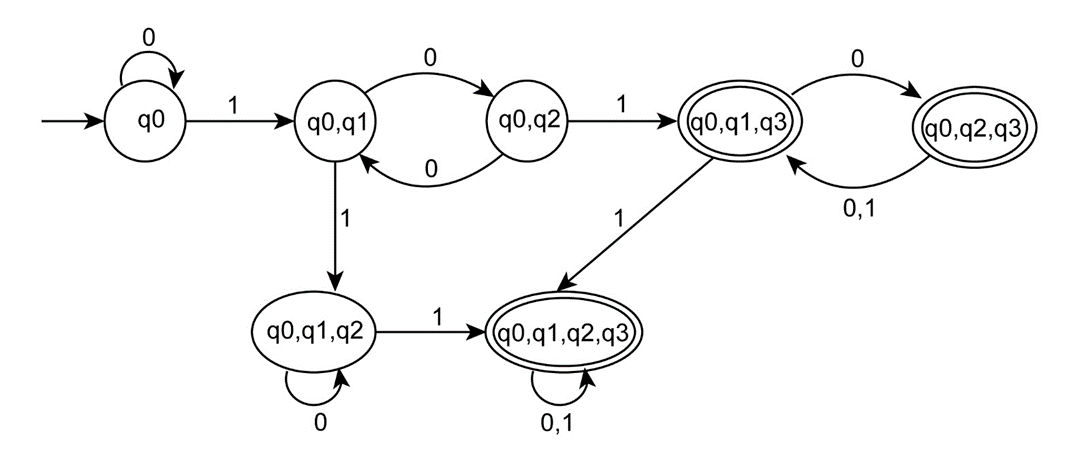
Change the final states to non-final states and vice versa to complement the above DFA as follows:

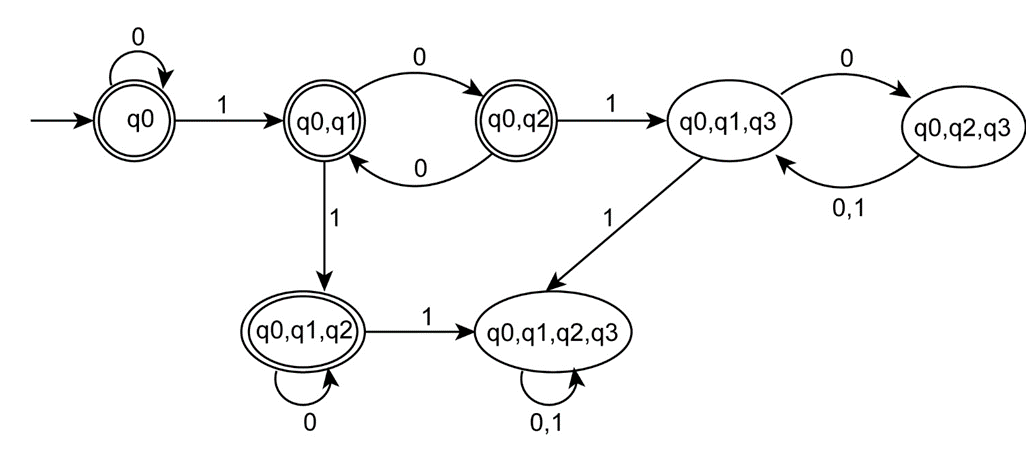
Combine the dead states in the above DFA as a single state as follows,

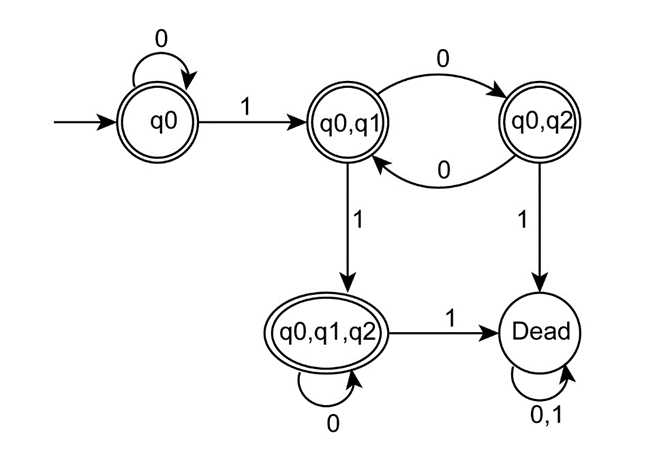
Simplify the above DFA by renaming the states as follows:

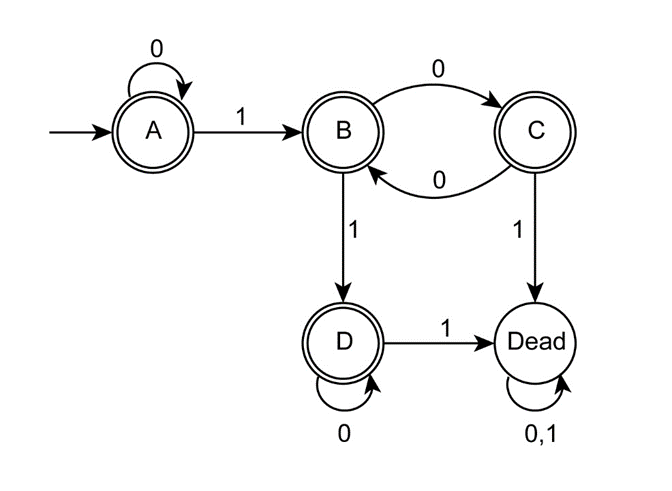
Therefore, the state diagram of a DFA with five states that recognizes has been obtained.