Prove that you can see all of yourself in a mirror that is only half as tall as you are. (Hint: Study the diagram on page 582.)

The given statement is you can see all of yourself in a mirror that is only half as tall as you are.

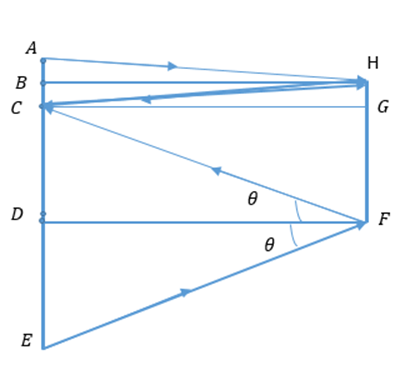
Consider you are standing in front of a mirror of height FH and your height is AE.

Point C represents your eye, A represents top of your head, E represents foot, B is the mid-point between your eye and top of your head, D is the mid-point between your eye and foot, F is the bottom of the mirror, H is the top of the mirror and G is a point in the mirror parallel to your eyes.

Since,

$\begin{array}{l}AE=AB+BC+CD+DE\\ AE=BC+BC+CD+CD\left[AB=BC,CD=DE\right]\\ AE=2\left(BC+CD\right)\left(i\right)\\ \text{and}\\ HF=HG+GF\left(ii\right)\end{array}$

In similar triangles CGF and CDF

$\begin{array}{l}CF\text{iscommonside}\\ CD=DF\\ \text{therefore},CD=GF\end{array}$

In similar triangles BCH and CGH

$\begin{array}{l}CH\text{iscommonside}\\ BH=CG\\ \text{therefore,}BC=HG\end{array}$

Substitute the values of HG and GF in equation i.

$\begin{array}{l}HF=HG+GF\left(ii\right)\\ HF=BC+CD\left[CD=GF,BC=HG\right]\\ HF=\frac{AE}{2}\left[AE=2\left(BC+CD\right)\right]\end{array}$

It is proved that you can see all of yourself in a mirror that is only half as tall as you are.