Use the “Initial Public Offering” data (see Appendix C) to test the claim that the mean offer price was \(\$18\) per share.

Do not use all the data. Use your random number generator to randomly survey \(15\) prices.

As per the information, I have to use the IPO data from appendix C to test the claim that the mean offer price is \(\$18\) per share. I have to randomly choose \(15\) prices from the data to do the hypothesis testing.

Hypothesis test is usually performed on a sample data taken from larger population. This test is used to obtain results based on a hypothesis performed on the sample data. Usually the analysts perform this test to determine whether his hypothesis is true or false.

Null hypothesis states that there is no statistical connection between two variables and hence the researcher always uses this to disapprove the inference. Alternate hypothesis states that there is a significant relationship between two variables.

Student’s t-distribution is also a part of continuous probability distribution methods which is used when the standard deviation value is unknown and the sample size for any given population is more than or equal to \(30\). This method is used again when the population is normally distributed for any sample size and the values of standard deviation is unknown.

First let us determine the null and alternate hypothesis:

Null hypothesis states that the mean offer price is \(\$18\) per share and the alternate hypothesis states that the mean offer price is different from \(\$18\0 per share.

\(H_{0}:\mu=18\)

\(H_{a}:\mu\neq 18\)

Here the random variable which is \(\bar{X}\), the mean offer price per share. Since we do not know the population standard deviation we use student’s t-distribution for this test.

\(t_{n-1}=t_{15-1}\)

\(=t_{14}\)

Thus the \(t\) test statistic is calculated using the following formula:

\(t=\frac{\bar{X}-\mu}{s/\sqrt{n}}\)

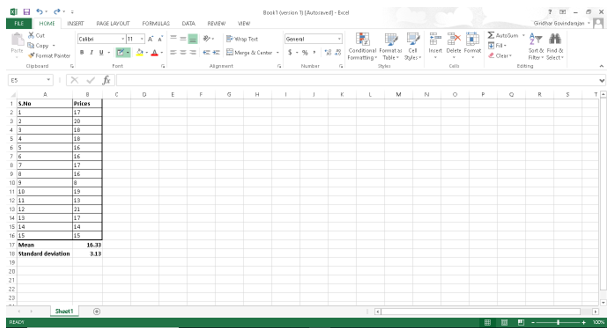
Here \(\bar{X}\) is the sample mean and \(\mu\) is the population mean, \(s\) is the standard deviation and n is the sample size. Now the randomly chosen \(15\) prices from appendix C is entered in Excel to calculate mean and standard deviation. The mean is calculated using the function =average ( ) and the standard deviation is calculate using the function =stdev ( ).

Therefore let us calculate t value in the t test statistic formula

\(t=\frac{\bar{X}-\mu}{s/\sqrt{n}}\)

\(=\frac{16.33-18}{3.13\sqrt{15}}\)

\(=\frac{-1.67}{3.13/3.8729}\)

\(=\frac{-1.69}{0.808}\)

\(=-2.066\)

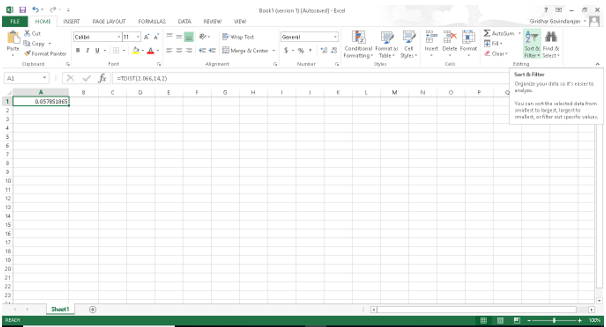
After this step let us find the r-value using TDISTfunction in excel.

Thus the following is the student’s t-distribution curve for the hypothesis test.

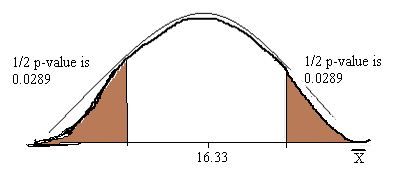
We know that alpha value is \(0.05\) and the \(p-\)value is less than the alpha value therefore the null hypothesis is rejected. Since null hypothesis is rejected we accept the alternate hypothesis since we have enough evidence to state that the mean offer price is different from \($18\) per share.

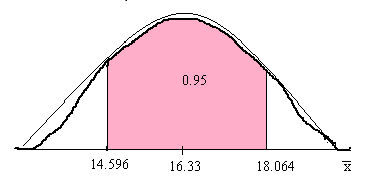
Now let us determine the \(95%\) confidence interval:

Thus the \(95%\) confidence level indicates that the mean offer price per share lies within \(14.596\) and \(18.064\). Let us represent the same in the student’s t-distribution curve