Question 9: Let \(S = \left\{ {\left( {x,y} \right):{x^{\bf{2}}} + {{\left( {y - {\bf{1}}} \right)}^2} \le {\bf{1}}} \right\} \cup \left\{ {\left( {{\bf{3}},{\bf{0}}} \right)} \right\}\). Is the origin an extreme point of \({\mathop{\rm conv}\nolimits} S\)? Is the origin a vertex of \({\mathop{\rm conv}\nolimits} S\)?

Theorem 15 states that consider \(S\) as a nonempty compact convex set.So, \(S\) is the convex hull of its profile (the set of extreme points of \(S\)).

Consider \(S\) as a convex set. A point pis referred to as extreme pointof \(S\) if pis not in the interior of any line segment that lies in \(S\).

More precisely, if \({\mathop{\rm x}\nolimits} ,y \in S\) and \({\bf{p}} \in \overline {{\mathop{\rm xy}\nolimits} } \), then \({\bf{p}} = {\mathop{\rm x}\nolimits} \) or \({\bf{p}} = {\mathop{\rm y}\nolimits} \). The set of all extreme points of \(S\)is called theprofileof \(S\).

The set \(S\) is convexif for each \({\bf{p}},{\bf{q}} \in S\), the line segment \(\overline {{\bf{pq}}} \) is contained in \(S\). The set of all convex combinations of points in a set \(S\) is called the convex hull of \(S\), represented by \({\mathop{\rm conv}\nolimits} S\).

Let \(S = \left\{ {\left( {x,y} \right):{x^2} + {{\left( {y - 1} \right)}^2} \le 1} \right\} \cup \left\{ {\left( {3,0} \right)} \right\}\).

The center of the equation \({{\mathop{\rm x}\nolimits} ^2} + {\left( {{\mathop{\rm y}\nolimits} - 1} \right)^2} = 1\) is \(\left( {0,1} \right)\) and radius is 1. Graph the set S as shown below:

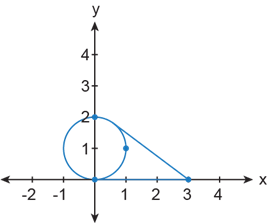
The point \(\left( {0,0} \right)\) is an extreme point of the \({\mathop{\rm conv}\nolimits} S\). It is not the interior of any line segment that lies in \(S\).

A line segment through the circle contains zero as an endpoint but \(\left( {0,0} \right)\) is not a vertex of the \({\mathop{\rm conv}\nolimits} S\).

The line segment passes from origin to the point \(\left( {3,0} \right)\). Therefore, the origin is an extreme point and not a vertex of the \({\mathop{\rm conv}\nolimits} S\).

Thus, the origin is an extreme point and not a vertex of the \({\mathop{\rm conv}\nolimits} S\).