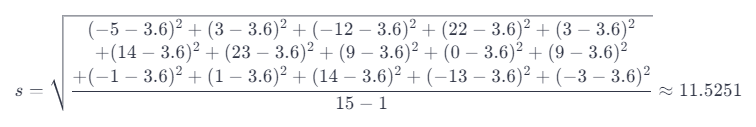A researcher wants to determine whether or not a five-week crash diet is effective over a long period of time. A random sample of 15 dieters is selected. Each person's weight is recorded before starting the diet and one year after it is concluded. Based on the data shown below (weight in pounds), can we conclude that the diet has a long-term effect, that is, that dieters managed to not regain the weight they lost? Include appropriate statistical evidence to justify your answer.

$n=\text{Sample size}=15$

$\alpha =\text{Significance level}=5\%=0.05$

Let us first determine the differences in value for each dieter.

The mean is the sum of all values divided by the number of values:

$$\begin{gathered} -5+3-12+22+3+14+23+9+0+9 \\ \overline{x}=\frac{-1+1+14-13-3}{15} \\ =\frac{54}{20} \\ =3.6 \end{gathered}$$

The variance is the sum of squared deviations from the mean divided by $n-1$. The standard deviation is the square root of variance.

The variance is the sum of squared deviations from the mean divided by $n-1$. The standard deviation is the square root of the variance:

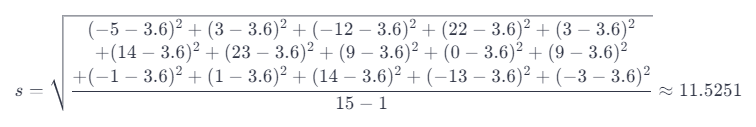
To use a paired t-test for the mean difference, we require that 3 conditions are satisfied: Random, $10\%$and Normal/Large sample

Random: Satisfied, because the sample is a random sample.

$10\%$: Satisfied, because the 15 dieters are less than $10\%$of all dieters

Normal/Random sample: Satisfied, because the normal probability plot of the differences does not contain strong curvature and this then implies data appears to originate from a population with approximately a normal distribution.

We then note that all three conditions are satisfied.

Given claim: Dieters manage to not regain the weight they lose or equivalently the mean difference After-Before is greater than 0 .

The claim is either the null hypothesis or the alternative hypothesis. The null hypothesis states that the population mean is equal to the value mentioned in the claim. If the null hypothesis is the claim, then the alternative hypothesis states the opposite of the null hypothesis.

$H_0:\mu =0$

$H_a:\mu >0$

Determine the value of the test statistic:

$t=\frac{\overline{x}-{\mu }_0}{s/\sqrt{n}}=\frac{3.6-0}{11.5251/\sqrt{15}}\approx 1.210$

The P-value is the probability of obtaining the value of the test statistic, or a value more extreme, assuming that the null hypothesis is true. The P-value is the number (or interval) in the column title of the Student's $\mathrm{T}$table in the appendix that contains the t-value in the row $df=n-1=15-1=14$:

$0.10<P<0.15$

If the P-value is smaller than the significance level $\alpha$, then the null hypothesis is rejected.

$P>0.05\Rightarrow \text{Fail to reject}{H}_0$