Learning Materials
Features
Discover
Chapter 7: Q.57 (page 455)
What does the CLT say? Asked what the central limit theorem says, a student replies, "As you take larger and larger samples from a population, the histogram of the sample values looks mote and more Normal." ls the student right? Explain your answer.
The student is not right
Over 30 million students worldwide already upgrade their learning with Vaia!
All the tools & learning materials you need for study success - in one app.
Get started for free
Tall girls According to the National Center for Health Statistics, the distribution of heights for 16-year-old females is modeled well by a Normal density curve with mean inches and standard deviation inches. To see if this distribution applies at their high school, an AP Statistics class takes an SRS of of the -year-old females at the school and measures their heights. What values of the sample mean x would be consistent with the population distribution being ? To find out, we used Fathom software to simulate choosing SRSs of size students from a population that is . The figure below is a dotplot of the sample mean height x of the students in the sample.
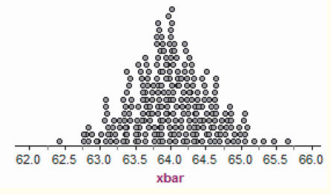
(a) Is this the sampling distribution of ? Justify your answer.
(b) Describe the distribution. Are there any obvious outliers?
(c) Suppose that the average height of the girls in the class’s actual sample is . What would you conclude about the population mean height for the -year-old females at the school? Explain.
Tall girls Refer to Exercise 10.
(a) Make a graph of the population distribution.
(b) Sketch a possible graph of the distribution of sample data for the SRS of size taken by the AP Statistics class.
Run a mile During World War II, able-bodied male undergraduates at the University of Illinois participated in required physical training. Each student ran a timed mile. Their times followed the Normal distribution with mean minutes and standard deviation minute. An SRS of of these students has mean time minutes. A second SRS of sizehas mean minutes. After many SRSs, the values of the sample mean x follow the Normal distribution with mean minutes and standard deviationminute.
(a) What is the population? Describe the population distribution. (b) Describe the sampling distribution of x. How is it different from the population distribution?
The candy machine Suppose a large candy machine has orange candies. Use Figure 7.13 (page 435) to help answer the following questions.
(a) Would you be surprised if a sample of 25 candies from the machine contained 8 orange candies (that's orange)? How about 5 orange candies ( orange)? Explain.
(b) Which is more surprising: getting a sample of 25 candies in which are orange or getting a sample of 50 candies in which are orange? Explain.
Airline passengers get heavier In response to the increasing weight of airline passengers, the Federal Aviation Administration (FAA) in told airlines to assume that passengers average pounds in the summer, including clothes and carry-on baggage. But passengers vary, and the FAA did not specify a standard deviation. A reasonable standard deviation is pounds. Weights are not Normally distributed, especially when the population includes both men and women, but they are not very non-Normal. A commuter plane carries passengers.
(a) Explain why you cannot calculate the probability that a randomly selected passenger weighs more than pounds.
(b) Find the probability that the total weight of the passengers on a full flight exceeds pounds. Show your work. (Hint: To apply the central limit theorem, restate the problem in terms of the mean weight.)
What do you think about this solution?
We value your feedback to improve our textbook solutions.
Explanations 
Textbooks 
Exams 
GCSE 
IGCSE 
AS 
A Level 
International A Level 
University Admissions Tests 
Flashcards 
Vaia AI 
Notes 
Study Plans 
Study Sets 
Find a job 
Find a degree 
Student Deals 
Magazine 
Mobile App