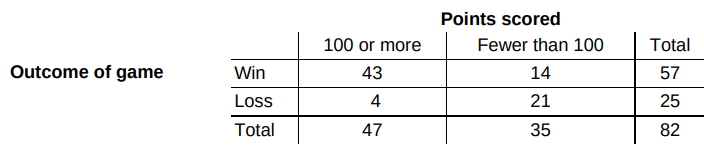The Dallas Mavericks won the NBA championship in the 2010–2011 season. The two-way table displays the relationship between the outcome of each game in the regular season and whether the Mavericks scored at least 100 points.
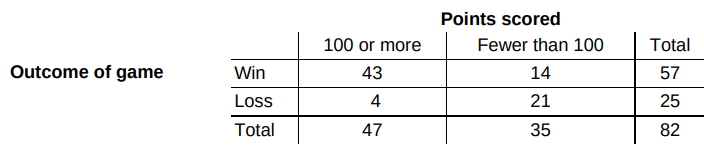
Which of the following is the best evidence that there is an association between the outcome of a game and whether or not the Mavericks scored at least 100 points?
(a) The Mavericks won 57 games and lost only 25 games.
(b) The Mavericks scored at least 100 points in 47 games and fewer than 100 points in only 35 games.
(c) The Mavericks won 43 games when scoring at least 100 points and only 14 games when scoring fewer than 100 points.
(d) The Mavericks won a higher proportion of games when scoring at least 100 points (43/47) than when they scored fewer than 100 points (14/35).
(e) The combination of scoring 100 or more points and winning the game occurred more often (43 times) than any other combination of outcomes.