Potato chips Refer to Exercise $47$ Use the $68–95–99.7$ rule to answer the

following questions.

a. About what percent of bags weigh less than $9.02$ ounces? Show your method clearly.

b. A bag that weighs$9.07$ ounces is at about what percentile in this distribution? Justify your answer.

Mean,$\mu =9.12$

Standard deviation,$\sigma =0.05$

Graph of normal probability- We can claim that the distribution is roughly Normal if the Normal probability plot has a linear structure.

According to $68-95-99.7$ rule:

In a normal distribution, $68$ percent of the data lies within $1$ standard deviation of the mean.

A normal distribution has $95$ percent of its data within two standard deviations of the mean.

A normal distribution has $99.7\%$ of its data inside $1$ standard deviation of the mean.

Then

The general Normal density graph is represented as:

Note that

$9.02$ lies $2\sigma$ below the mean.

$\mu -2\sigma =9.12-2(0.05)=9.02$

According to $68-95-99.7$ rule:

95% of the data values are within $2$ standard deviations of the mean. $68-95-99.7$n.

Although,

Data values in total are $100\%$

Then

$100\%-95\%=5\%$

$5\%$ of the data values are greater than $2$ standard deviations off the mean.

We also know that

The normal distribution is symmetric around the mean.

That implies

$2.5$ percent of the data points are more than $2$ standard deviations above the mean.

And

$2.5$ percent of the data points are more than $2$ standard deviations below the mean.

Therefore,

$2.5\%$ of the bags weigh less than $9.02$ ounces.

According to $68-95-99.7$ rule:

In a normal distribution, $68$ percent of the data lies within $1$ standard deviation of the mean.

In a normal distribution, $95\%$ of the data lies within $2$ standard deviations of the mean.

A normal distribution has $99.7\%$ of its data inside $1$ standard deviation of the mean.

Then

The general Normal density graph is represented as:

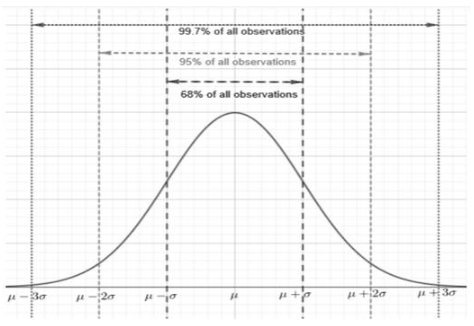
Note that

$9.02$ lies $\sigma$ below the mean.

According to $68-95-99.7$ rule:

$68\%$ of the data values lie within $\sigma$ ($1$ standard deviation) of the mean.

Although,

Data values in total are $100\%$

Then

$\mu -\sigma =9.12-0.05=9.07$

According to $68-95-99.7$ rule:

$68\%$ of the data values lie within $\sigma$ ($1$ standard deviation) of the mean.

Although,

Data values in total are $100\%$

Then

$100\%-68\%=32\%$

$32\%$ of the data values lie more than $\sigma$ ($1$ standard deviation) from the mean.

We also know that

The normal distribution is symmetric about the mean.

That implies

$16\%$ of the data values are more than $\sigma$ ($1$ standard deviation) above the mean.

We also know that

The normal distribution is symmetric about the mean.

That implies

$16\%$ of the data values are more than $\sigma$ ($1$ standard deviation) above the mean.

And

$16\%$ of the data values are more than $\sigma$ ($1$ standard deviation) below the mean.

The data value represented by the $Xth$ percentile includes $x\%$ of the data values below it.

That implies

Bag that weighs $9.07$ ounces has about $16\%$ of the other weighs below it.

Thus,

The bag is at $16th$ percentile.