Consider two insulating balls with evenly distributed equal and opposite charges on their surfaces, held with a certain distance between the centers of the balls. Construct a problem in which you calculate the electric field (magnitude and direction) due to the balls at various points along a line running through the centers of the balls and extending to infinity on either side. Choose interesting points and comment on the meaning of the field at those points. For example, at what points might the field be just that due to one ball and where does the field become negligibly small? Among the things to be considered are the magnitudes of the charges and the distance between the centers of the balls. Your instructor may wish for you to consider the electric field off axis or for a more complex array of charges, such as those in a water molecule.

A system consists of two equal but opposite nature of charge separated by some distance is called electric dipole.

Consider two metal balls having charges \( + 5{\rm{ C}}\) and \( - 5{\rm{ C}}\) are separated by \(6{\rm{ m}}\). (a) Find the magnitude of electric field between half way of the charges. (b) Find the magnitude of electric field at any point \(4{\rm{ m}}\) on the equatorial line. (c) Find the magnitude of electric field either on both side at distance of \(15{\rm{ m}}\) on the line joining both charges.

The electric field in the half way of the charges is represented as,

Here, \({E_1}\) is the electric field due to \( + 5{\rm{ C}}\), \({E_2}\) is the electric field due to \( - 5{\rm{ C}}\), and \(r\) is the separation between \( + 5{\rm{ C}}\) and \( - 5{\rm{ C}}\).

The electric field due to \( + 5{\rm{ C}}\) is,

\({E_1} = \frac{{K\left| {5{\rm{ C}}} \right|}}{{{{\left( {\frac{r}{2}} \right)}^2}}}\)

Here, \(K\) is the electrostatic force constant.

Substitute \(9 \times {10^9}{\rm{ N}} \cdot {{\rm{m}}^2}/{{\rm{C}}^2}\) for \(K\), and \(6{\rm{ m}}\) for \(r\),

\(\begin{array}{c}{E_1} = \frac{{\left( {9 \times {{10}^9}{\rm{ N}} \cdot {{\rm{m}}^2}/{{\rm{C}}^2}} \right) \times \left| {5{\rm{ C}}} \right|}}{{{{\left( {\frac{{6{\rm{ m}}}}{2}} \right)}^2}}}\\ = 5 \times {10^9}{\rm{ N}}/{\rm{C}}\end{array}\)

The electric field due to \( - 5{\rm{ C}}\) is,

\({E_2} = \frac{{K\left| { - 5{\rm{ C}}} \right|}}{{{{\left( {\frac{r}{2}} \right)}^2}}}\)

Here, \(K\) is the electrostatic force constant.

Substitute \(9 \times {10^9}{\rm{ N}} \cdot {{\rm{m}}^2}/{{\rm{C}}^2}\) for \(K\), and \(6{\rm{ m}}\) for \(r\),

\(\begin{array}{c}{E_2} = \frac{{\left( {9 \times {{10}^9}{\rm{ N}} \cdot {{\rm{m}}^2}/{{\rm{C}}^2}} \right) \times \left| { - 5{\rm{ C}}} \right|}}{{{{\left( {\frac{{6{\rm{ m}}}}{2}} \right)}^2}}}\\ = 5 \times {10^9}{\rm{ N}}/{\rm{C}}\end{array}\)

At the center, the net electric field is,

\(E = {E_1} + {E_2}\)

Substitute \(5 \times {10^9}{\rm{ N}}/{\rm{C}}\)for\({E_1}\)and\(5 \times {10^9}{\rm{ N}}/{\rm{C}}\)for\({E_2}\),

\(\begin{array}{c}E = \left( {5 \times {{10}^9}{\rm{ N}}/{\rm{C}}} \right) + \left( {5 \times {{10}^9}{\rm{ N}}/{\rm{C}}} \right)\\ = {10^{10}}{\rm{ N}}/{\rm{C}}\end{array}\)

Hence, the electric field in the halfway of the charges is \({10^{10}}{\rm{ N}}/{\rm{C}}\).

The electric field on the equatorial line is represented as,

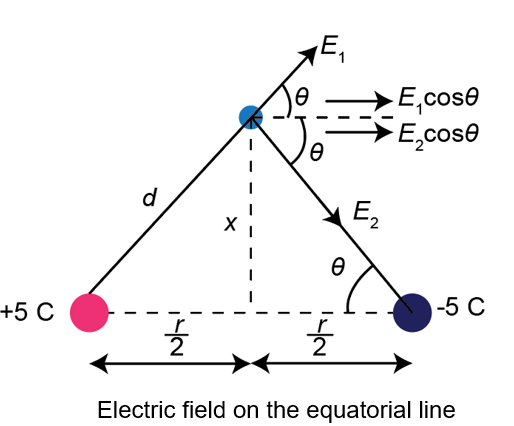
Here, \({E_1}\) is the electric field due to \( + 5{\rm{ C}}\), \({E_2}\) is the electric field due to \( - 5{\rm{ C}}\), and \(r\) is the separation between \( + 5{\rm{ C}}\) and \( - 5{\rm{ C}}\), \(x\) is the distance of the point from the equatorial line.

The distance of the point from the charge is,

\(d = \sqrt {{{\left( {\frac{r}{2}} \right)}^2} + {x^2}} \)

Substitute \(6{\rm{ m}}\) for \(r\), and \(4{\rm{ m}}\) for \(x\),

\(\begin{array}{c}d = \sqrt {{{\left( {\frac{{6{\rm{ m}}}}{2}} \right)}^2} + {{\left( {4{\rm{ m}}} \right)}^2}} \\ = 5{\rm{ m}}\end{array}\)

The electric field due to \( + 5{\rm{ C}}\) is,

\({E_1} = \frac{{K\left| {5{\rm{ C}}} \right|}}{{{d^2}}}\)

Here, \(K\) is the electrostatic force constant.

Substitute \(9 \times {10^9}{\rm{ N}} \cdot {{\rm{m}}^2}/{{\rm{C}}^2}\) for \(K\), and \({\rm{5 m}}\) for \(d\),

\(\begin{array}{c}{E_1} = \frac{{\left( {9 \times {{10}^9}{\rm{ N}} \cdot {{\rm{m}}^2}/{{\rm{C}}^2}} \right) \times \left| {5{\rm{ C}}} \right|}}{{{{\left( {5{\rm{ m}}} \right)}^2}}}\\ = 1.8 \times {10^9}{\rm{ N}}/{\rm{C}}\end{array}\)

The electric field due to \( - 5{\rm{ C}}\) is,

\({E_2} = \frac{{K\left| { - 5{\rm{ C}}} \right|}}{{{d^2}}}\)

Here, \(K\) is the electrostatic force constant.

Substitute \(9 \times {10^9}{\rm{ N}} \cdot {{\rm{m}}^2}/{{\rm{C}}^2}\) for \(K\), and \({\rm{5 m}}\) for \(d\),

\(\begin{array}{c}{E_2} = \frac{{\left( {9 \times {{10}^9}{\rm{ N}} \cdot {{\rm{m}}^2}/{{\rm{C}}^2}} \right) \times \left| { - 5{\rm{ C}}} \right|}}{{{{\left( {5{\rm{ m}}} \right)}^2}}}\\ = 1.8 \times {10^9}{\rm{ N}}/{\rm{C}}\end{array}\)

From geometry,

\(\cos \theta = \frac{{r/2}}{d}\)

Substitute \(6{\rm{ m}}\) for \(r\), and \(5{\rm{ m}}\) for \(d\),

\(\begin{array}{c}\cos \theta = \frac{{\left( {6{\rm{ m}}/2} \right)}}{{5{\rm{ m}}}}\\ = 0.6\end{array}\)

Due to symmetry of the system, the horizontal component of the field cancels each other. Therefore, the net electric field at the point on equatorial line is,

\(\begin{array}{c}E = {E_1}\cos \theta + {E_2}\cos \theta \\ = \left( {{E_1} + {E_2}} \right)\cos \theta \end{array}\)

Substitute \(1.8 \times {10^9}{\rm{ N}}/{\rm{C}}\) for \({E_1}\), \(1.8 \times {10^9}{\rm{ N}}/{\rm{C}}\) for \({E_2}\), and \(0.6\) for \(\cos \theta \),

\(\begin{array}{c}E = \left[ {\left( {1.8 \times {{10}^9}{\rm{ N}}/{\rm{C}}} \right) + \left( {1.8 \times {{10}^9}{\rm{ N}}/{\rm{C}}} \right)} \right] \times 0.6\\ = 2.16 \times {10^9}{\rm{ N}}/{\rm{C}}\end{array}\)

Hence, the electric field strength at a distance the \(4{\rm{ m}}\) on the equatorial line is \(2.16 \times {10^9}{\rm{ N}}/{\rm{C}}\).

The electric field is represented as,

Here, \({E_1}\) is the electric field due to \( + 5{\rm{ C}}\), \({E_2}\) is the electric field due to \( - 5{\rm{ C}}\), and \(r\) is the separation between \( + 5{\rm{ C}}\) and \( - 5{\rm{ C}}\), \(d\) is the charge.

The electric field due to \( + 5{\rm{ C}}\) is,

\({E_1} = \frac{{K\left| {5{\rm{ C}}} \right|}}{{{{\left( {r + d} \right)}^2}}}\)

Here, \(K\) is the electrostatic force constant.

Substitute \(9 \times {10^9}{\rm{ N}} \cdot {{\rm{m}}^2}/{{\rm{C}}^2}\) for \(K\), \(6{\rm{ m}}\) for \(r\), and \({\rm{15 m}}\) for \(d\),

\(\begin{array}{c}{E_1} = \frac{{\left( {9 \times {{10}^9}{\rm{ N}} \cdot {{\rm{m}}^2}/{{\rm{C}}^2}} \right) \times \left| {5{\rm{ C}}} \right|}}{{{{\left[ {\left( {{\rm{6 m}}} \right) + \left( {15{\rm{ m}}} \right)} \right]}^2}}}\\ = 1.02 \times {10^8}{\rm{ N}}/{\rm{C}}\end{array}\)

The electric field due to \( - 5{\rm{ C}}\) is,

\({E_2} = \frac{{K\left| { - 5{\rm{ C}}} \right|}}{{{d^2}}}\)

Substitute \(9 \times {10^9}{\rm{ N}} \cdot {{\rm{m}}^2}/{{\rm{C}}^2}\) for \(K\), and \({\rm{15 m}}\) for \(d\),

\(\begin{array}{c}{E_2} = \frac{{\left( {9 \times {{10}^9}{\rm{ N}} \cdot {{\rm{m}}^2}/{{\rm{C}}^2}} \right) \times \left| { - 5{\rm{ C}}} \right|}}{{{{\left( {15{\rm{ m}}} \right)}^2}}}\\ = 2 \times {10^8}{\rm{ N}}/{\rm{C}}\end{array}\)

The magnitude of electric field at distance of \(15{\rm{ m}}\) is,

\(E = \left| {{E_1} - {E_2}} \right|\)

Substitute \(1.02 \times {10^8}{\rm{ N}}/{\rm{C}}\) for \({E_1}\) and \(2 \times {10^8}{\rm{ N}}/{\rm{C}}\) for \({E_2}\),

\(\begin{array}{c}E = \left| {\left( {1.02 \times {{10}^8}{\rm{ N}}/{\rm{C}}} \right) - \left( {2 \times {{10}^8}{\rm{ N}}/{\rm{C}}} \right)} \right|\\ = 9.8 \times {10^7}{\rm{ N}}/{\rm{C}}\end{array}\)

When the test charge is on the right side of the \( + 5{\rm{ C}}\), due to the symmetry of the system the electric field is \(9.8 \times {10^7}{\rm{ N}}/{\rm{C}}\).

Hence, the magnitude of the electric field \(9.8 \times {10^7}{\rm{ N}}/{\rm{C}}\).