Point charges of\(25.0{\rm{ }}\mu {\rm{C}}\)and\(45.0{\rm{ }}\mu {\rm{C}}\)are placed\(0.500{\rm{ m}}\)apart. (a) At what point along the line between them is the electric field zero? (b) What is the electric field halfway between them?

The space around the charge in which another charge experiences some electrostatic force of attraction or repulsion is known as electric field.The expression for the electric field is,

\(E = \frac{{Kq}}{{{r^2}}}\)

Here,\(K\)is the electrostatic force constant,\(q\)is the magnitude of the charge and\(r\)is the distance of the point of consideration from the charge.

The electric field is a vector quantity. For a system of charges, the electric field at a point equals the vector sum of all the electric field acting at that point.

Let the electric field be zero at point x from the \(25.0{\rm{ }}\mu C\). The electric field at x is represented as,

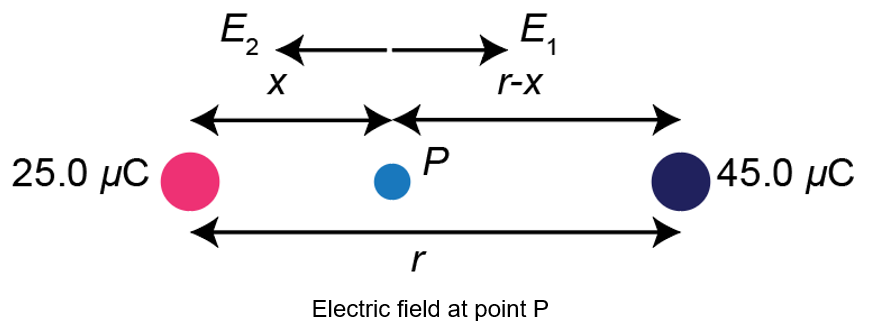
Here,\({E_1}\)is the electric field due to the charge\(25.0{\rm{ \mu C}}\),\({E_2}\)is the electric field due to the charge\(45.0{\rm{ \mu C}}\), and\(r\)is the distance between\(25.0{\rm{ \mu C}}\)and\(45.0{\rm{ \mu C}}\).

The electric field due to the charge\(25.0{\rm{ \mu C}}\)is,

\({E_1} = \frac{{K\left( {25.0{\rm{ }}\mu {\rm{C}}} \right)}}{{{x^2}}}\)

The electric field due to the charge\(45.0{\rm{ \mu C}}\)is,

\({E_2} = \frac{{K\left( {45.0{\rm{ }}\mu {\rm{C}}} \right)}}{{{{\left( {r - x} \right)}^2}}}\)

The net electric field at point P is,

\(\begin{array}{c}E = {E_1} - {E_2}\\ = \frac{{K\left( {25.0{\rm{ }}\mu {\rm{C}}} \right)}}{{{x^2}}} - \frac{{K\left( {45.0{\rm{ }}\mu {\rm{C}}} \right)}}{{{{\left( {r - x} \right)}^2}}}\end{array}\)

Since, the net electric field at point P is zero i.e.,\(E = 0\). Therefore,

\(\begin{array}{c}0 = \frac{{K\left( {25.0{\rm{ \mu C}}} \right)}}{{{x^2}}} - \frac{{K\left( {45.0{\rm{ \mu C}}} \right)}}{{{{\left( {r - x} \right)}^2}}}\\\frac{{K\left( {25.0{\rm{ \mu C}}} \right)}}{{{x^2}}} = \frac{{K\left( {45.0{\rm{ \mu C}}} \right)}}{{{{\left( {r - x} \right)}^2}}}\\{\left( {\frac{{r - x}}{x}} \right)^2} = \frac{{45}}{{25}}\end{array}\)

Therefore, the expression for\(x\)(distance where electric field is zero from\(25.0{\rm{ \mu C}}\)) is,

\(\begin{array}{c}\frac{r}{x} - 1 = \sqrt {\frac{{45}}{{25}}} \\\frac{r}{x} = \sqrt {\frac{{45}}{{25}}} + 1\\x = \frac{r}{{\sqrt {\frac{{45}}{{25}}} + 1}}\end{array}\)

Substitute\(0.500{\rm{ m}}\)for\(r\),

\(\begin{array}{c}x = \frac{{0.500{\rm{ m}}}}{{\sqrt {\frac{{45}}{{25}}} + 1}}\\ = 0.214{\rm{ m}}\end{array}\)

Hence, the electric field will be zero at \(0.214{\rm{ m}}\) from the \(25.0{\rm{ \mu C}}\).

The electric field in the half way of the charges is represented as,

Here,\({E_1}\)is the electric field due to the charge\(25.0{\rm{ \mu C}}\),\({E_2}\)is the electric field due to the charge\(45.0{\rm{ \mu C}}\), and\(r\)is the distance between\(25.0{\rm{ \mu C}}\)and\(45.0{\rm{ \mu C}}\).

The electric field due to the charge\(25.0{\rm{ \mu C}}\)is,

\({E_1} = \frac{{K\left( {25.0{\rm{ }}\mu {\rm{C}}} \right)}}{{{{\left( {\frac{r}{2}} \right)}^2}}}\)

The electric field due to the charge\(45.0{\rm{ \mu C}}\)is,

\({E_2} = \frac{{K\left( {45.0{\rm{ }}\mu {\rm{C}}} \right)}}{{{{\left( {\frac{r}{2}} \right)}^2}}}\)

The net electric field at point P is,

Substitute\(9 \times {10^9}{\rm{ N}} \cdot {{\rm{m}}^{\rm{2}}}{\rm{/}}{{\rm{C}}^{\rm{2}}}\)for\(K\), and\(0.500\,{\rm{m}}\)for r,

\(\begin{array}{c}E = \frac{{\left( {9 \times {{10}^9}{\rm{ N}} \cdot {{\rm{m}}^{\rm{2}}}{\rm{/}}{{\rm{C}}^{\rm{2}}}} \right) \times \left( { - 20.0{\rm{ }}\mu {\rm{C}}} \right)}}{{{{\left( {\frac{{0.500}}{2}} \right)}^2}}}\\ = \frac{{\left( {9 \times {{10}^9}{\rm{ N}} \cdot {{\rm{m}}^{\rm{2}}}{\rm{/}}{{\rm{C}}^{\rm{2}}}} \right) \times \left( { - 20.0{\rm{ }}\mu {\rm{C}}} \right) \times \left( {\frac{{{{10}^{ - 6}}{\rm{ C}}}}{{1{\rm{ }}\mu {\rm{C}}}}} \right)}}{{{{\left( {\frac{{0.500}}{2}} \right)}^2}}}\\ = - 2.88 \times {10^6}{\rm{ N}}/{\rm{C}}\end{array}\)

Here, the negative sign indicates that the electric field is directed away from the\(45.0{\rm{ \mu C}}\)charge.

Hence, the electric field in the half way between the charges is\(2.88 \times {10^6}{\rm{ N}}/{\rm{C}}\)directed away from the\(45.0{\rm{ \mu C}}\).