Show that the order of addition of three vectors does not affect their sum. Show this property by choosing any three vectors \({\rm{A}}\), \({\rm{B}}\), and \({\rm{C}}\), all having different lengths and directions. Find the sum \({\rm{A}} + {\rm{B}} + {\rm{C}}\) then find their sum when added in a different order and show the result is the same. (There are five other orders in which \({\rm{A}}\), \({\rm{B}}\), and \({\rm{C}}\) can be added; choose only one.)

Two vectors can be added together by placing them together in such a way that the tail of the second vector is connected to the head of the first vector. Thus, by joining the tail of the first vector to the head of the second vector, the resultant of the two vectors can be obtained.

Consider vector \({\rm{A}}\) having magnitude of \(3\;{\rm{m}}\) towards east, vector \({\rm{B}}\) having magnitude of \(4\;{\rm{m}}\) towards north, and vector \({\rm{C}}\) having magnitude \(5\;{\rm{m}}\) towards west.

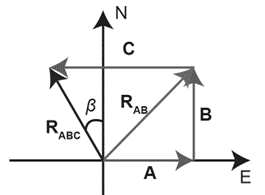
Fig: Vector representation of \({\rm{A}} + {\rm{B}} + {\rm{C}}\)

Vectors \({\rm{A}}\) and \({\rm{B}}\) are perpendicular to each other. The resultant of vector \({\rm{A}}\) and \({\rm{B}}\)is,

\({{\rm{R}}_{{\rm{AB}}}} = \sqrt {{{\left| {\rm{A}} \right|}^2} + {{\left| {\rm{B}} \right|}^2} + 2\left| {\rm{A}} \right|\left| {\rm{B}} \right|\cos \left( {{{90}^ \circ }} \right)} \)

Substitute the values in the above expression, and we get,

\(\begin{aligned}{}{{\rm{R}}_{{\rm{AB}}}} &= \sqrt {{{\left( {3\;{\rm{m}}} \right)}^2} + {{\left( {4\;{\rm{m}}} \right)}^2} + 2 \times \left( {3\;{\rm{m}}} \right) \times \left( {4\;{\rm{m}}} \right) \times \cos \left( {{{90}^ \circ }} \right)} \\ &= 5\;{\rm{m}}\end{aligned}\)

The direction of resultant of vectors \({\rm{A}}\) and \({\rm{B}}\)is,

\(\alpha = {\tan ^{ - 1}}\left( {\frac{{\left| {\rm{B}} \right|}}{{\left| {\rm{A}} \right|}}} \right)\)

Substitute the values in the above expression, and we get,

\(\begin{aligned}{}\alpha &= {\tan ^{ - 1}}\left( {\frac{{4\;{\rm{m}}}}{{3\;{\rm{m}}}}} \right)\\ = {53.13^ \circ }\end{aligned}\)

Thus, the resultant of vectors \({\rm{A}}\) and \({\rm{B}}\) is \(5\;{\rm{m}}\) and directed towards \({53.13^ \circ }\) the north of east.

The angle between resultant of vectors \({\rm{A}}\) and \({\rm{B}}\) \(\left( {{{\rm{R}}_{{\rm{AB}}}}} \right)\), and vector \({\rm{C}}\) is,

\(\theta = {180^ \circ } - \alpha \)

Substitute \({53.13^ \circ }\) for \(\alpha \), and we get,

\(\begin{aligned}{}\theta = {180^ \circ } - {53.13^ \circ }\\ = {126.87^ \circ }\end{aligned}\)

The resultant of vectors \({{\rm{R}}_{{\rm{AB}}}}\)and\({\rm{C}}\)is,

\({{\rm{R}}_{{\rm{ABC}}}} = \sqrt {{{\left| {{{\rm{R}}_{{\rm{AB}}}}} \right|}^2} + {{\left| {\rm{C}} \right|}^2} + 2\left| {{{\rm{R}}_{{\rm{AB}}}}} \right|\left| {\rm{C}} \right|\cos \theta } \)

Substitute the values in the above expression, and we get,

\(\begin{aligned}{}{{\rm{R}}_{{\rm{ABC}}}} &= \sqrt {{{\left( {5\;{\rm{m}}} \right)}^2} + {{\left( {5\;{\rm{m}}} \right)}^2} + 2 \times \left( {5\;{\rm{m}}} \right) \times \left( {5\;{\rm{m}}} \right) \times \cos \left( {{{126.87}^ \circ }} \right)} \\ &= 4.47\;{\rm{m}}\end{aligned}\)

The direction of resultant \({{\rm{R}}_{{\rm{ABC}}}}\)is,

\(\begin{aligned}{}\beta &= {\tan ^{ - 1}}\left( {\frac{{2\;{\rm{m}}}}{{4\;{\rm{m}}}}} \right)\\ &= {26.57^ \circ }\end{aligned}\)

Hence, the resultant of\({\rm{A}} + {\rm{B}} + {\rm{C}}\)is \(4.47\;{\rm{m}}\) and directed \({26.57^ \circ }\) west of north.

The sum of the vectors \({\rm{A}} + {\rm{C}} + {\rm{B}}\)is represented as,

Vector representation of \({\rm{A}} + {\rm{C}} + {\rm{B}}\)

Vectors \({\rm{A}}\) and \({\rm{C}}\) are opposite to each other. Thus, the resultant of vectors \({\rm{A}}\) and \({\rm{C}}\) is,

\({{\rm{R}}_{{\rm{AC}}}} = \sqrt {{{\left| {\rm{A}} \right|}^2} + {{\left| {\rm{C}} \right|}^2} + 2\left| {\rm{A}} \right|\left| {\rm{C}} \right|\cos \left( {{{180}^ \circ }} \right)} \)

Substitute the values in the above expression, and we get,

\(\begin{aligned}{}{{\rm{R}}_{{\rm{AC}}}} &= \sqrt {{{\left( {3\;{\rm{m}}} \right)}^2} + {{\left( {5\;{\rm{m}}} \right)}^2} + 2 \times \left( {3\;{\rm{m}}} \right) \times \left( {5\;{\rm{m}}} \right) \times \cos \left( {{{180}^ \circ }} \right)} \\ &= 2\;{\rm{m}}\end{aligned}\)

Since the magnitude of the vector \({\rm{C}}\) is greater than the magnitude of the vector \({\rm{A}}\). Thus, the resultant \({{\rm{R}}_{{\rm{AC}}}}\) is directed towards the west.

Vectors \({{\rm{R}}_{{\rm{AC}}}}\) and \({\rm{B}}\) are perpendicular to each other. The resultant of vector \({{\rm{R}}_{{\rm{AC}}}}\) and \({\rm{B}}\) is,

\({{\rm{R}}_{{\rm{ACB}}}} = \sqrt {{{\left| {{{\rm{R}}_{{\rm{AC}}}}} \right|}^2} + {{\left| {\rm{B}} \right|}^2} + 2\left| {{{\rm{R}}_{{\rm{AC}}}}} \right|\left| {\rm{B}} \right|\cos \left( {{{90}^ \circ }} \right)} \)

Substitute the values in the above expression, and we get,

\(\begin{aligned}{}{{\rm{R}}_{{\rm{ACB}}}} &= \sqrt {{{\left( {2\;{\rm{m}}} \right)}^2} + {{\left( {4\;{\rm{m}}} \right)}^2} + 2 \times \left( {2\;{\rm{m}}} \right) \times \left( {4\;{\rm{m}}} \right) \times \cos \left( {{{90}^ \circ }} \right)} \\ &= 4.47\;{\rm{m}}\end{aligned}\)

The direction of resultant \({{\rm{R}}_{{\rm{ABC}}}}\)is,

\(\gamma = {\tan ^{ - 1}}\left( {\frac{{\left| {{{\rm{R}}_{{\rm{AC}}}}} \right|}}{{\left| {\rm{B}} \right|}}} \right)\)

Substitute the values in the above expression, and we get,

\(\begin{aligned}{}\gamma &= {\tan ^{ - 1}}\left( {\frac{{2\;{\rm{m}}}}{{4\;{\rm{m}}}}} \right)\\ &= {26.57^ \circ }\end{aligned}\)

Thus, \({\rm{A}} + {\rm{B}} + {\rm{C}} = {\rm{A}} + {\rm{C}} + {\rm{B}}\). Hence, the order of addition of three vectors does not affect their sum.