Learning Materials
Features
Discover
Chapter 6: Q18 CQ (page 220)
A non-rotating frame of reference placed at the centre of the Sun is very nearly an inertial one. Why is it not exactly an inertial frame?
The non-rotating frame will also wobble a bit and hence would not be completely inertial.
Over 30 million students worldwide already upgrade their learning with Vaia!
All the tools & learning materials you need for study success - in one app.
Get started for free
(a) Calculate the magnitude of the acceleration due to gravity on the surface of Earth due to the Moon. (b) Calculate the magnitude of the acceleration due to gravity at Earth due to the Sun. (c) Take the ratio of the Moon’s acceleration to the Sun’s and comment on why the tides are predominantly due to the Moon in spite of this number.
Calculate the centripetal force on the end of a \(100{\rm{ m}}\) (radius) wind turbine blade that is rotating at \(0.5{\rm{ rev}}/{\rm{s}}\). Assume the mass is \(4{\rm{ kg}}\).
An automobile with 0.260 m radius tires travels80,000km before wearing them out. How many revolutions do the tires make, neglecting any backing up and any change in radius due to wear?
A large centrifuge, like the one shown in Figure (a), is used to expose aspiring astronauts to accelerations similar to those experienced in rocket launches and atmospheric re-entries. (a) At what angular velocity is the centripetal acceleration \(10g\) if the rider is \(15.0{\rm{ m}}\) from the centre of rotation? (b) The rider’s cage hangs on a pivot at the end of the arm, allowing it to swing outward during rotation as shown in Figure (b). At what angle \(\theta \) below the horizontal will the cage hang when the centripetal acceleration is \(10g\)? (Hint: The arm supplies centripetal force and supports the weight of the cage. Draw a free body diagram of the forces to see what the angle \(\theta \) should be.)
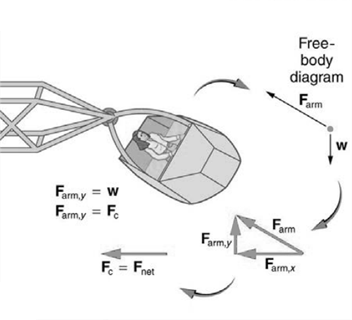
*Figure (a) NASA centrifuge used to subject trainees to accelerations similar to those experienced in rocket launches and re-entries. (Credit: NASA) (b) Rider in cage showing how the cage pivots outward during rotation. This allows the total force exerted on the rider by the cage to be along its axis at all times.
If centripetal force is directed toward the centre, why do you feel that you are ‘thrown’ away from the centre as a car goes around a curve? Explain.
What do you think about this solution?
We value your feedback to improve our textbook solutions.
Explanations 
Textbooks 
Exams 
GCSE 
IGCSE 
AS 
A Level 
International A Level 
University Admissions Tests 
Flashcards 
Vaia AI 
Notes 
Study Plans 
Study Sets 
Find a job 
Find a degree 
Student Deals 
Magazine 
Mobile App