Learning Materials
Features
Discover
Chapter 6: Q6.3-3CQ (page 218)
If you wish to reduce the stress (which is related to centripetal force) on high-speed tires, would you use large- or small-diameter tires? Explain.
Centripetal is the force that acted on a body in a circle always the effective inward direction of the circular path.
Over 30 million students worldwide already upgrade their learning with Vaia!
All the tools & learning materials you need for study success - in one app.
Get started for free
A number of amusement parks have rides that make vertical loops like the one shown in Figure. For safety, the cars are attached to the rails in such a way that they cannot fall off. If the car goes over the top at just the right speed, gravity alone will supply the centripetal force. What other force acts and what is its direction if: (a) The car goes over the top at faster than this speed? (b)The car goes over the top at slower than this speed?
(a) What is the acceleration due to gravity on the surface of the Moon?
(b) On the surface of Mars? The mass of Mars is \({\bf{6}}.{\bf{418}} \times {\bf{1}}{{\bf{0}}^{{\bf{23}}}}{\bf{kg}}\) and its radius is\({\bf{3}}.{\bf{38}} \times {\bf{1}}{{\bf{0}}^{\bf{6}}}{\bf{m}}\).
When a toilet is flushed or a sink is drained, the water (and other material) begins to rotate about the drain on the way down. Assuming no initial rotation and a flow initially directly straight toward the drain, explain what causes the rotation and which direction it has in the northern hemisphere. (Note that this is a small effect and in most toilets the rotation is caused by directional water jets.) Would the direction of rotation reverse if water were forced up the drain?
Part of riding a bicycle involves leaning at the correct angle when making a turn, as seen in Figure. To be stable, the force exerted by the ground must be on a line going through the center of gravity. The force on the bicycle wheel can be resolved into two perpendicular components—friction parallel to the road (this must supply the centripetal force), and the vertical normal force (which must equal the system’s weight).
(a) Show that\(\theta \)(as defined in the figure) is related to the speed v and radius of curvature r of the turn in the same way as for an ideally banked roadway—that is,\(\theta = {\tan ^{ - 1}}\,{v^2}/rg\)
(b) Calculate \(\theta \) for a \(12.0{\rm{ m}}/{\rm{s}}\) turn of radius \(30.0{\rm{ m}}\) (as in a race).
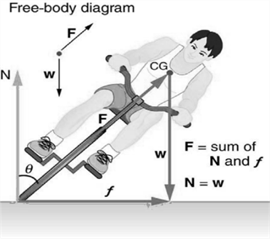
Figure 6.36 A bicyclist negotiating a turn on level ground must lean at the correct angle—the ability to do this becomes instinctive. The force of the ground on the wheel needs to be on a line through the center of gravity. The net external force on the system is the centripetal force. The vertical component of the force on the wheel cancels the weight of the system while its horizontal component must supply the centripetal force. This process produces a relationship among the angle \(\theta \), the speed \(v\), and the radius of curvature \(r\) of the turn similar to that for the ideal banking of roadways.
Space debris left from old satellites and their launchers is becoming a hazard to other satellites
(a) Calculate the speed of a satellite in an orbit900 km above Earth’s surface.
(b) Suppose a loose rivet is in an orbit of the same radius that intersects the satellite’s orbit at an angle ofrelative to Earth. What is the velocity of the rivet relative to the satellite just before striking it?
(c) Given the rivet is 3.00 mmin size, how long will its collision with the satellite last?
(d) If its mass is0.500 g, what is the average force it exerts on the satellite? (e) How much energy in joules is generated by the collision? (The satellite’s velocity does not change appreciably, because its mass is much greater than the rivet’s.)
What do you think about this solution?
We value your feedback to improve our textbook solutions.
Explanations 
Textbooks 
Exams 
GCSE 
IGCSE 
AS 
A Level 
International A Level 
University Admissions Tests 
Flashcards 
Vaia AI 
Notes 
Study Plans 
Study Sets 
Find a job 
Find a degree 
Student Deals 
Magazine 
Mobile App