Log out Go to App
Go to App

Learning Materials

Features

Discover

Chapter 22: Q58P (page 657)

A certain electric dipole is placed in a uniform electric field E→of magnitude.20N/CFigure 22-62 gives the potential energy of the dipole versus the angle u between E and the dipole momentp→. The vertical axis scale is set byUs=1.00×10−28J.What is the magnitude of p→?

Short Answer

Expert verified

The magnitude of dipole momentp→ is.5.00×10−28C.m

Step by step solution

01

The given data

  1. Electric field of magnitude,E=20N/C
  2. And the above graph,Us=1.00×10−28J
02

Understanding the concept of energy of the electric dipole

The potential energy of the electric dipole placed in an electric field depends on its orientation relative to the electric field.The magnitude of the electric dipole moment isp=qd, where q is the magnitude of the charge, and d is the separation between the two charges.

Formula:

When placed in an electric field, the potential energy of the dipole,

(i)

U(θ)=−p→.E→=−pEcosθ

03

Calculation of magnitude of the dipole moment

Examining the lowest value on the graph, we have the magnitude of the dipole moment using equation (i) as:

U=−p→.E→−1.00×10−28J=−20N/C(p→)p→=5.00×10−28C.m

Hence, the value of the dipole moment is.5.00×10−28C.m

Unlock Step-by-Step Solutions & Ace Your Exams!

  • Full Textbook Solutions

    Get detailed explanations and key concepts

  • Unlimited Al creation

    Al flashcards, explanations, exams and more...

  • Ads-free access

    To over 500 millions flashcards

  • Money-back guarantee

    We refund you if you fail your exam.

Start your free trial

Over 30 million students worldwide already upgrade their learning with Vaia!

One App. One Place for Learning.

All the tools & learning materials you need for study success - in one app.

Get started for free

Most popular questions from this chapter

A charge (uniform linear density=9.0nC/m) lies on a string that is stretched along an xaxis fromx=0tox=3.0m. Determine the magnitude of the electric field atx=4.0mon the xaxis.

A clock face has negative point charges,-q,−2q, −3q. . . ,−12qfixed at the positions of the corresponding numerals. The clock hands do not perturb the net field due to the point charges. At what time does the hour hand point in the same direction as the electric field vector at the center of the dial? (Hint:Use symmetry.)

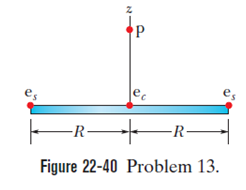
Figure 22-40 shows a proton (p) on the central axis through a disk with a uniform charge density due to excess electrons. The disk is seen from an edge-on view. Three of those electrons are shown: electron ecat the disk center and electrons esat opposite sides of the disk, at radius Rfrom the center. The proton is initially at distance z=R=2.00 cmfrom the disk. At that location, what are the magnitudes of (a) the electric field Ec→ due to electron ecand (b) the netelectric field E→s,net due to electrons es? The proton is then moved to z=R/10.0. What then are the magnitudes of (c) E→cand E→s,net (d) at the proton’s location? (e) From (a) and (c) we see that as the proton gets nearer to the disk, the magnitude of E→cincreases, as expected. Why does the magnitude of E→s,net from the two side electrons decrease, as we see from (b) and (d)?

An electron with a speed of 5.00×108cm/s enters an electric field of magnitude1.00×103N/C , traveling along a field line in the direction that retards its motion. (a) How far will the electron travel in the field before stopping momentarily, and (b) how much time will have elapsed? (c) If the region containing the electric field is8.00 mm long (too short for the electron to stop within it), what fraction of the electron’s initial kinetic energy will be lost in that region?

Figure 22-26 shows two charged particles fixed in place on an axis. (a) Where on the axis (other than at an infinite distance) is there a point at which their net electric field is zero: between the charges, to their left, or to their right? (b) Is there a point of zero net electric field anywhere offthe axis (other than at an infinite distance)?
See all solutions

Recommended explanations on Physics Textbooks

Famous Physicists

Read Explanation

Conservation of Energy and Momentum

Read Explanation

Solid State Physics

Read Explanation

Quantum Physics

Read Explanation

Work Energy and Power

Read Explanation

Engineering Physics

Read Explanation
View all explanations

What do you think about this solution?

We value your feedback to improve our textbook solutions.

Study anywhere. Anytime. Across all devices.

Sign-up for free