Question:In Figure, four long straight wires are perpendicular to the page, and their cross sections form a square of edge length $\mathit{a}\mathbf{=}\mathbf{}\mathbf{20}\mathbf{}\mathbf{\text{cm}}$. The currents are out of the page in wires 1 and 4 and into the page in wires 2 and 3, and each wire carries 20 A. In unit-vector notation, what is the net magnetic field at the square’s center?

i) The current carrying wires are perpendicular to the page

ii) The current in each wire = 20A.

iii) The distance between wires = edge length of square = $20 \text{cm} \text{or} 0.2 \text{m}$.

iv) The currents in wires 1 and 4 are out of page, and those in wires 2 and 3 are into the page.

The net magnetic field at the center of the square is the vector sum of the magnetic fields of all 4 wires. We can determine the magnetic field of each wire by using the formula for the magnetic field at some point outside the current-carrying wire. Adding them will give the magnetic field at the center of the square.

Formula:

$B=\frac{{\mu }_{0}i}{2\pi R}$

Where is the magnetic permeability of free space$(4\pi \times {10}^{-7}{\text{NA}}^{\text{- 2}})$.

The magnetic field at the center of the square is the vector sum of the magnetic field of all 4 wires. We use the Biot-Savart law to determine the magnetic field of the wires. For all the wires, the distance of the center from the wire is the same = R. It is related to edge length as

$\begin{array}{rcl}R& =& \frac{\text{diagonal}}{\text{2}}\\ & =& \frac{a\sqrt{2}}{2}\\ & =& \frac{a}{\sqrt{2}}\end{array}$

The magnetic field due to wire 1 is calculated as

$B=\frac{{\mu }_{0}i}{2\pi R}$

$\begin{array}{rcl}{B}_1& =& \frac{{\mu }_{0}i}{2\pi \left(\frac{a}{\sqrt{2}}\right)}\\ & =& \frac{{\mu }_{0}i\sqrt{2}}{2\pi a}\end{array}$

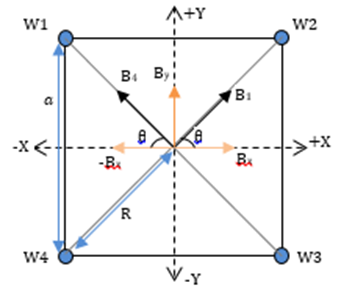
The current in the wire 1 is directed out of the page. Hence the direction of the magnetic field at the center is determined using the right hand rule. According to the rule, the direction of this field will be in the counter clockwise direction. So at the center it will be along the diagonal of the square, perpendicular to R. Hence it will have components along +x and +Y direction.

The magnitude of the magnetic field will bethesame for wire 4. The direction of this field will be in the counter clockwise direction. But at the center, it will be along the diagonal such that it has components along -X and +Y direction (as shown in the diagram).

The magnitude of the magnetic field will bethesame for wire 2 and wire 3 as well. But for these wires, the current is going into the page. The direction of this field will be in the clockwise direction. At the center, the field due to wire 2 will be same as B₄ and that for wire 3 will be same as B₁.

Looking at the diagram, we can see that the x components of the four fields will be directed in opposite directions along the X axis. Henceit will get cancelled. The Y components of all the fields are along the same direction (+Y). Hence resultant field will be the sum of these components. The Y component will be given by

$\begin{array}{rcl}{B}_{1y}& =& B_{3y}\\ & =& \frac{{\mu }_{0}i\sqrt{2}}{2\pi a}\sin 45\end{array}$

$\begin{array}{rcl}{B}_{2y}& =& B_{4y}\\ & =& \frac{{\mu }_{0}i\sqrt{2}}{2\pi a}\sin (90+45)\\ & =& \frac{{\mu }_{0}i\sqrt{2}}{2\pi a}\cos 45°\end{array}$

Hence the net magnetic field at the center is

$B=B_{1y}+B_{2y}+B_{3y}+B_{4y}$

$\therefore B=4\left(\frac{{\mu }_{0}i\sqrt{2}}{2\pi a}\times \frac{1}{\sqrt{2}}\right)$

Note here that;

$\begin{array}{rcl}\sin 45°& =& \cos 45°\\ & =& \frac{1}{\sqrt{2}}\end{array}$

$B=\frac{4\times \left(4\pi \times {10}^{-7} \text{N} {\text{A}}^{\text{- 2}}\right)\times \left(20 \text{A}\right)}{2\pi \times \left(20\times {10}^{-2} \text{m}\right)}$

$$\begin{gathered} B=80\times {10}^{-6}T \\ B=80\mu T \end{gathered}$$