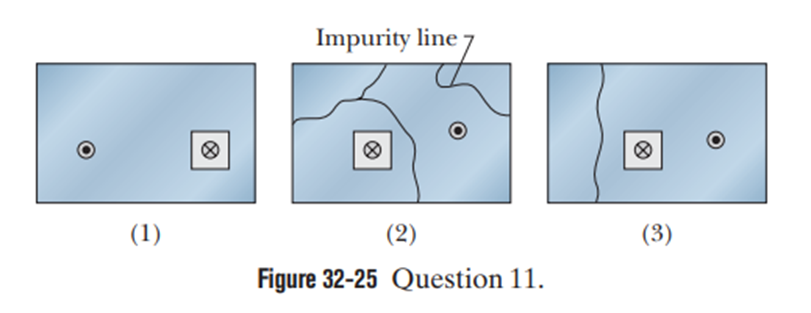
Figure 32-25 represents three rectangular samples of a ferromagnetic material in which the magnetic dipoles of the domains have been directed out of the page (encircled dot) by a very strong applied field B0 . In each sample, an island domain still has its magnetic field directed into the page (encircled X ). Sample 1 is one (pure) crystal. The other samples contain impurities collected along lines; domains cannot easily spread across such lines.
The applied field is now to be reversed and its magnitude kept moderate. The change causes the island domain to grow. (a) Rank the three samples according to the success of that growth, greatest growth first. Ferromagnetic materials in which the magnetic dipoles are easily changed are said to be magnetically soft; when the changes are difficult, requiring strong applied fields, the materials are said to be magnetically hard. (b) Of the three samples, which is the most magnetically hard?