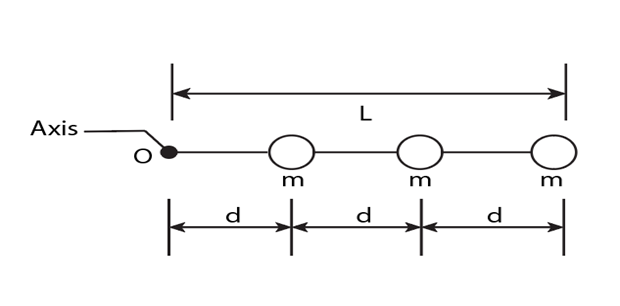
In Fig. , three particles have been glued to a rod of length and negligible mass and can rotate around a perpendicular axis through point at one end. How much work is required to change the rotational rate
(a) from torole="math" localid="1660925307834" ,
(b) fromto, and
(c) fromto?
(d) What is the slope of a plot of the assembly’s kinetic energy (in joules) versus the square of its rotation rate (in radians squared per second squared)?