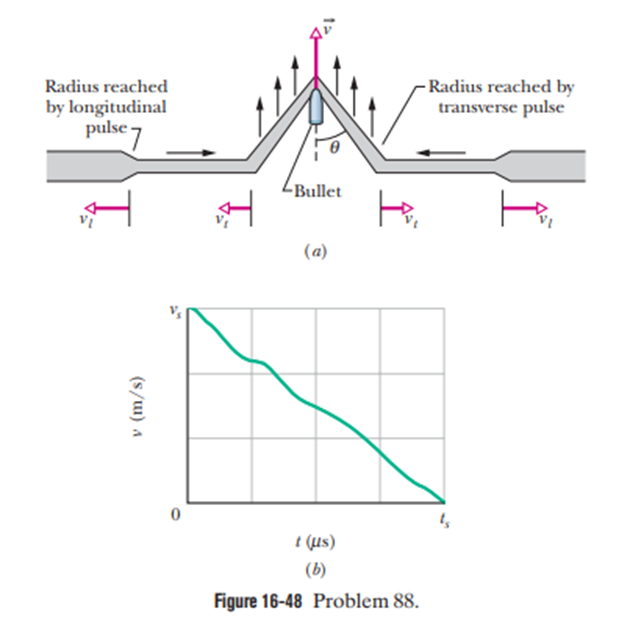
Body armor. When a high-speed projectile such as a bullet or bomb fragment strikes modern body armor, the fabric of the armor stops the projectile and prevents penetration by quickly spreading the projectile’s energy over a large area. This spreading is done by longitudinal and transverse pulses that move radiallyfrom the impact point, where the projectile pushes a cone-shaped dent into the fabric. The longitudinal pulse, racing along the fibers of the fabric at speedahead of the denting, causes the fibers to thin and stretch, with material flowing radially inward into the dent. One such radial fiber is shown in Fig. 16-48a. Part of the projectile’s energy goes into this motion and stretching. The transverse pulse, moving at a slower speed, is due to the denting. As the projectile increases the dent’s depth, the dent increases in radius, causing the material in the fibers to move in the same direction as the projectile (perpendicular to the transverse pulse’s direction of travel). The rest of the projectile’s energy goes into this motion. All the energy that does not eventually go into permanently deforming the fibers ends up as thermal energy. Figure 16-48bis a graph of speed vversus time tfor a bullet of mass 10.2g fired from a .38 Special revolver directly into body armor. The scales of the vertical and horizontal axes are set byand. Take, and assume that the half-angle of the conical dent is. At the end of the collision, what are the radii of (a) the thinned region and (b) the dent (assuming that the person wearing the armor remains stationary)?