A particle of mass m and charge q is attached to a spring with force constant k, hanging from the ceiling (Fig. 11.18). Its equilibrium position is a distance h above the floor. It is pulled down a distance d below equilibrium and released, at time.
(a) Under the usual assumptions , calculate the intensity of the radiation hitting the floor, as a function of the distance R from the point directly below q. [Note: The intensity here is the average power per unit area of floor.]
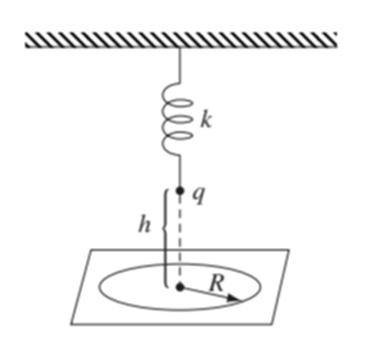
FIGURE 11.18
At whatR is the radiation most intense? Neglect the radiative damping of the oscillator.
(b) As a check on your formula, assume the floor is of infinite extent, and calculate the average energy per unit time striking the entire floor. Is it what you’d expect?
(c) Because it is losing energy in the form of radiation, the amplitude of the oscillation will gradually decrease. After what timehas the amplitude been reduced to ? (Assume the fraction of the total energy lost in one cycle is very small.)


