Chapter 16: Q12Q (page 662)

Location A is a distance d from a charged particle. Location B is a distance 2d from the particle. Which of the following statements are true? It may help to draw a diagram. (1) If the charge of the particle is negative, $V_{B} - V_{A}$ is negative. (2) If the charge of the particle is positive, $(V_{A} < V_{B})$ . (3) If $V_{B} < V_{A}$ , we know that the particle must be positive. (4) $V_{B} < V_{A}$ , regardless of the sign of the charge of the particle. (5) The sign of $(V_{B} - V_{A})$ does not give us any information about the sign of the charge of the particle.

Short Answer

Expert verified

The correct answer is statement (3).

Step by step solution

Identification of given data

The given data can be listed below,

The distance of location A from the charge particle is, d.
The distance of the location/point B from the charge particle is, 2d.

Concept/Significance of the unit charge.

The property of matter that produces an electric field is known as charge. The electron has a negative charge, while the proton has a positive charge, according to tradition. The fact that they have opposing charges attracts them.

Determination of the correct statement.

1. The electric field will be to the left if the particle is negative, as indicated in the diagram below.

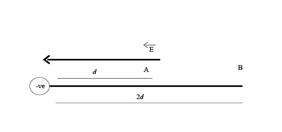
The potential difference is travelling from point A to point B. The potential is positive because it is in the opposite direction of the electric field. This option is incorrect.

2. The electric field will be to the right if the particle is positive, as indicated in the diagram below.

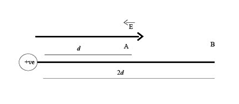
As a result, point A has a positive value, while point B has a negative value. The potential at the positive point is greater than the potential at the negative point in this scenario. So, in order for the potential difference to be positive, the potential at position A must be larger than the potential at position B $(V_{A} > V_{B})$ , so, this option is incorrect.

3. As explained in part (2), as the particle is positive the potential at point B is less than the potential at point A $(V_{A} > V_{B})$

Thus, this statement (3) is correct i.e., when $V_{A} > V_{B}$ the particle must be positive.

4. The direction of the electric field is changed by the sign of the particle, and the sign of the potential difference is changed by the direction of the electric field.so, the statement is proved incorrect.

5. it is explained in the previous parts that the potential difference depends on the sign of the particle and the statement is not justifying it because it is saying the potential does not depend on the sign of charge which is incorrect. So, this statement is incorrect.

Thus, the correct answer is statement (3).