A straight circular plastic cylinder of length L and radius R ( where R<<L) is irradiated with a bean of protons so that there is a total excess charge Q distributed uniformly throughout the cylinder. Find the electric field inside the cylinder, a distance r from the center of the cylinder far from the ends, where r < R.

A straight circular plastic cylinder of length L and radius R ( where R << L) is irradiated with a bean of protons so that there is a total excess charge Q distributed uniformly throughout the cylinder.

The electric field$\overrightarrow{E}$ in the region is given by the expression $\oint \overrightarrow{E}·\hat{n}dA=\frac{q_{\text{inside}}}{{\epsilon }_0}$.

Gauss law related the flux through a surface and the net charge enclosed by the surface. So, here the normal vector to the surface is $\hat{n}$, the area of the Gaussian surface is dA. If the medium in between the conductors in air, therefore, the permittivity of free space is ${\epsilon }_0$. But if the medium happens to be other than air, like plastic, as stated in the problem, the equation may be written as:

$\oint \overrightarrow{E}·\hat{n}dA=\frac{q_{\text{inside}}}{\epsilon }\left(1\right)$

Here, the permittivity of the medium is $\epsilon$.

The plastic cylinder of radius R is given a positive charge -Q by irradiating it with protons and the charge is distributed in the volume of the cylinder. If its length be L, then, the charge per unit volume of the cylinder$\rho$is given by:

$\rho =\frac{Q}{\pi R^{2}L}$

A Gaussian cylinder of radius such that will be:

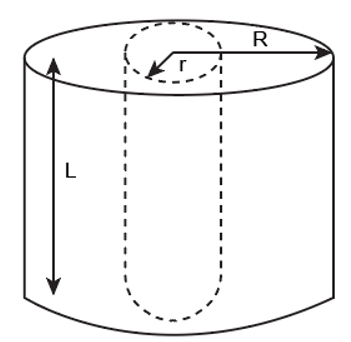
The charge contained by the Gaussian surface $q_{\text{inside}}$is given by:

$$\begin{gathered} q_{\text{inside}}=\rho \left(\pi r^{2}L\right) \\ {q}_{\text{inside}}=\frac{Q}{\pi R^{2}L}\left(\pi r^{2}L\right) \\ {q}_{\text{inside}}=\frac{Q{r}^2}{R^2} \end{gathered}$$

The electric field at a distance from the center is given by using this expression in equation (1) as:

$$\begin{gathered} \oint \overrightarrow{E}·\hat{n}dA=\frac{q_{\text{inside}}}{\epsilon } \\ \oint \overrightarrow{E}·\hat{n}dA=\frac{Q{r}^2}{R^2\epsilon }\left(2\right) \end{gathered}$$

The electric flux emerges out normally from the surface, therefore, the angle $\theta$between $\overrightarrow{E}$and $\hat{n}$is zero. So:

$$\begin{gathered} \overrightarrow{E}·\hat{n}dA=EdA\cos \theta \\ \overrightarrow{E}·\hat{n}dA=EdA \end{gathered}$$

The electric field is constant over the surface therefore:

$\overrightarrow{E}\oint dA=\frac{Q{r}^2}{R^2\epsilon }\left(3\right)$

The surface area of the Gaussian cylinder of the radius r and length L is given by:

$\oint dA=2\pi rL$

Thus the equation (3) will be:

$E\left(2\pi rL\right)=\frac{Q{r}^2}{R^2\epsilon }$

Now solving for E as:

$$\begin{gathered} E=\frac{Q{r}^2}{2\pi rL{R}^2\epsilon } \\ E=\frac{Qr}{2\pi L{R}^2\epsilon } \end{gathered}$$

Therefore, the electric field in the interior of the plastic cylinder is $E=\frac{Qr}{2\pi L{R}^2\epsilon }$.