You hold up an object that consists of two blocks at rest, each of mass, connected by a low-mass spring. Then you suddenly start applying a larger upward force of constant magnitude(which is greater than). Figureshows the situation some time later, when the blocks have moved upward, and the spring stretch has increased.
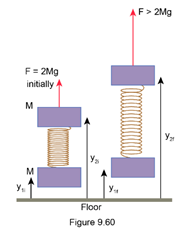
The heights of the centers of the two blocks are as follows:
Initial and final positions of block 1:
Initial and final positions of block 2:
It helps to show these heights on a diagram. Note that the initial center of mass of the two blocks is, and the final center of mass of the two blocks isrole="math" localid="1656911769231" . (a) Consider the point particle system corresponding to the two blocks and the spring. Calculate the increase in the total translational kinetic energy of the two blocks. It is important to draw a diagram showing all of the forces that are acting, and through what distance each force acts. (b) Consider the extended system corresponding to the two blocks and the spring. Calculate the increase of, the vibrational kinetic energy of the two blocks (their kinetic energy relative to the center of mass) plus the potential energy of the spring. It is important to draw a diagram showing all of the forces that are acting, and through what distance each force acts.



