Two identical 15.0 - kg balls, each 25.0 cm in diameter, are suspended by two 35.0 - cm wires (Fig. P5.85). The entire apparatus is supported by a single 18.0 - cm wire, and the surfaces of the balls are perfectly smooth. (a) Find the tension in each of the three wires. (b) How hard does each ball push on the other one?

The given data can be listed below as:

• The mass of both balls is $m_1=m_2=1.50kg$.
• The diameter of both balls is $d=25.0cm\times \frac{{10}^{-2}m}{1cm}=25\times {10}^{-2}m$.
• The length of the wires is $l_1=l_2=35.0cm\times \frac{{10}^{-1}m}{1cm}=35\times {10}^{-2}m$.

The length of the single wire is$l=18.0cm\times \frac{{10}^{-2}m}{1cm}=18\times {10}^{-2}m$ .

Tension is described as the force that is used to push or pull a particular object. The tension is also helpful for identifying the force exerted on an object.

The free body diagram of the system is drawn below:

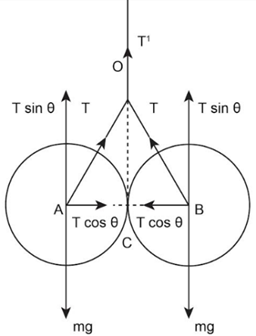
From the above diagram, it can be identified that there are three tensions acting such as T , T and T' . The tension acting on both the balls are equal but the total tension T' is the addition of the weight of the balls.

The equation of the Tension of the first ball is expressed as:

$$\begin{gathered} T\sin \theta =mg \\ T=\frac{mg}{\sin \theta }........\left(1\right) \end{gathered}$$

Here, $\theta$is the angle made by the first ball with the horizontal, m is the mass of the first ball, g is the acceleration due to gravity and T is the tension made by the first ball.

From the above diagrams, the angle made by the first ball can be identified with the help of Pythagoras’ theorem.

The straight line starting from the end of the wire to the center of the ball is described as the perpendicular line. According to the Pythagoras’ theorem, the straight line is described as the root of the subtraction of the square between the length of the first wire and the radius of the ball.

The equation of the angle subtended by the first ball is expressed as:

$\sin \theta =\frac{\sqrt{l_1^2-{\left({\displaystyle \frac{d}{2}}\right)}^2}}{l_1}$…(ii)

Here, $l_1$ is the length of the first wire and d is the diameter of the ball.

Substitute the values in the above equation.

$$\begin{gathered} \sin \theta =\frac{\sqrt{{\left(0.35m\right)}^2-{\left({\displaystyle \frac{0.25m}{2}}\right)}^2}}{\left(0.35m\right)} \\ =\frac{\sqrt{\left(0.1225m^2\right)-\left(0.015m^2\right)}}{\left(0.35m\right)} \\ =\frac{\sqrt{\left(0.1075m^2\right)}}{\left(0.35m\right)} \\ =\frac{0.32m}{\left(0.35m\right)} \\ =0.934 \end{gathered}$$

Substitute 0.934 for $\sin \theta$,$9.8m/s^2$ for g and 15.0 kg for m in the equation (i).

$$\begin{gathered} T=\frac{\left(15.0kg\right)\left(9.8m/s^2\right)}{0.934} \\ =\frac{\left(147kg.m/s^2\right)}{0.934} \\ =157kg.m/s^2\times \frac{1N}{1kg.m/s^2} \\ =157N \end{gathered}$$

Hence, it is the tension in both the wires.

The equation of the tension in the third wire is expressed as:

$$\begin{gathered} T\text{'}=mg+mg \\ =2mg \end{gathered}$$

Here, T' the tension in the third wire.

Substitute the values in the above equation.

$$\begin{gathered} T\text{'}=2\left(15kg\right)\left(9.8m/s^2\right) \\ =\left(30kg\right)\left(9.8m/s^2\right) \\ =294kg.m/s^2\times \frac{1N}{1kg.m/s^2} \\ =294N \end{gathered}$$

Thus, the tension in each three wires are 294 N , 157 N and 157 N respectively.

From the free body diagram, the equation of the force one ball pushes the other with is expressed as:

$$\begin{gathered} F=T\cos \theta \\ =T\sqrt{1-{\sin }^2\theta } \end{gathered}$$

Here, F is the force one ball pushes the other with.

Substitute the values in the above equation.

$$\begin{gathered} F=157N\sqrt{1-{\left(0.934\right)}^2} \\ =157N\sqrt{1-0.872} \\ =157N\sqrt{0.13} \\ =157N\times 0.36 \\ =56.60N \end{gathered}$$

Thus, each ball pushes the other ball with a force of 56.60 N .