Two identical thin rods, each with mass m and length L, are joined at right angles to form an L-shaped object. This object is balanced on top of a sharp edge (Fig. P14.88). If the L-shaped object is deflected slightly, it oscillates. Find the frequency of oscillation.

\(\begin{array}{l}{\rm{mass}}\;{\rm{of}}\;{\rm{each}}\;{\rm{rod}} = m\\{\rm{length}} = L\\{\rm{angle}} = 90^\circ \end{array}\)

The frequency of oscillation is calculated by how many waves completes the oscillation per unit time.

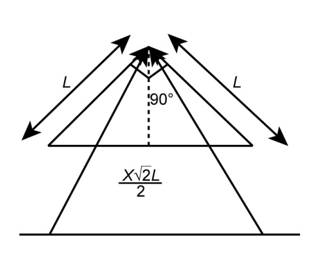
From the figure, the third side of the right angled triangle is

\(x = \sqrt {{L^2} + {L^2}} \)

x= third side of the right angled triangle.

\(\begin{array}{c}x = \sqrt {2{L^2}} \\ = \sqrt 2 \;L\end{array}\)

The center of gravity balanced by the rod is,

\(\begin{array}{l}d = \frac{L}{{2\sqrt 2 }}\\d = {\rm{balanced}}\;{\rm{distance}}\;{\rm{of}}\;{\rm{the}}\;{\rm{rods}}\end{array}\)

Moment of inertia is,

\(I = \frac{2}{3}m{L^2}\)

Frequency of oscillation of thin two rods is,

\(\begin{array}{c}f = \frac{1}{{2\pi }}\sqrt {\frac{{2mgd}}{I}} \;\;\;\;\;\;\;\;\;\;\left( {d = \frac{L}{{2\sqrt 2 }};\;I = \frac{2}{3}m{L^2}} \right)\\f = \frac{1}{{2\pi }}\sqrt {\frac{{2mg\left( {\frac{L}{{2\sqrt 2 }}} \right)}}{{\frac{2}{3}m{L^2}}}} \\ = \frac{1}{{2\pi }}\sqrt {\frac{{6g}}{{4\sqrt 2 \;L}}} \\ = \frac{1}{{4\pi }}\sqrt {\frac{{6g}}{{\sqrt 2 \;L}}} \end{array}\)

Hence the frequency of oscillation is \(\frac{1}{{4\pi }}\sqrt {\frac{{6g}}{{\sqrt 2 \;L}}} \)