56. A uniform disk with a radius \(R = 0.400{\rm{ m}}\) and mass \({\rm{30}}{\rm{.0 kg}}\) rotates in a horizontal plane on a frictionless vertical axle that passes through the center of the disk. The angle through which the disk has turned varies with time according to \(\theta \left( t \right) = \left( {1.10{{{\rm{ rad}}} \mathord{\left/ {\vphantom {{{\rm{ rad}}} {\rm{s}}}} \right.} {\rm{s}}}} \right)t + \left( {6.30{{{\rm{ rad}}} \mathord{\left/ {\vphantom {{{\rm{ rad}}} {{{\rm{s}}^{\rm{2}}}}}} \right.} {{{\rm{s}}^{\rm{2}}}}}} \right){t^2}\). What is the resultant linear acceleration of a point on the rim of the disk at the instant when the disk has turned through \({\rm{0}}{\rm{.100 rev}}\)?

Here,

The radius, \(R = 0.40{\rm{0 m}}\)

The mass, \(m = 30.{\rm{0 kg}}\)

Therefore,

\(\begin{aligned}\theta \left( t \right) = \left( {1.{\rm{10 }}\frac{{{\rm{rad}}}}{{\rm{s}}}} \right)t + \left( {6.{\rm{30 }}\frac{{{\rm{rad}}}}{{{{\rm{s}}^{\rm{2}}}}}} \right){t^2}\\\theta = 0.1{\rm{00 rev}}\left( {\frac{{2\pi {\rm{ rad}}}}{{1\,\,\,{\rm{rev}}}}} \right)\end{aligned}\)

Obtain the value of \(t\) if \(\theta = 0.6{\rm{28 rad}}\) as follows:

\(\begin{aligned}0.628 = 1.10t + 6.30{t^2}\\6.30{t^2} + 1.10t - 0.628 = 0\end{aligned}\)

Use the quadratic formula to solve the equation as follows:

\(\begin{aligned}t = \frac{{ - 1.10 \pm \sqrt {{{\left( {1.10} \right)}^2} - 4\left( {6.30} \right)\left( { - 0.628} \right)} }}{{2\left( {6.30} \right)}}\\ = \frac{{ - 1.1 \pm \sqrt {17.0356} }}{{12.6}}\end{aligned}\)

\(t = 0.240{\rm{ s}}\,\,\,{\mathop{\rm or}\nolimits} \,\,\,\,t = - 0.415{\rm{ s}}\)

Since \(t \ge 0\), ignore the negative value.

Therefore, the time is,

\(t = 0.240{\rm{ s}}\)

Obtain the constant angular acceleration as follows:

\(\begin{aligned}{w_z} = \frac{{d\theta }}{{dt}}\\ = 1.10 + 12.60t\end{aligned}\)

\(\begin{aligned}{w_z}\left( {0.240} \right) = 1.10 + 12.60\left( {0.240} \right)\\ = 4.1{\rm{24 }}\frac{{{\rm{rad}}}}{{\rm{s}}}\end{aligned}\)

The constant angular acceleration is as follows:

\(\begin{aligned}{\alpha _z} = \frac{{d{w_z}}}{{dt}}\\ = 12.{\rm{60 }}\frac{{{\rm{rad}}}}{{{{\rm{s}}^{\rm{2}}}}}\,\,\,\left( {{\mathop{\rm constant}\nolimits} \,\,\,{\mathop{\rm angular}\nolimits} \,\,{\mathop{\rm acceleration}\nolimits} } \right)\end{aligned}\)

Obtain the radial acceleration of a point on the rim of the disk at the instant as follows:

\(\begin{aligned}{a_{Rad}} = w_z^2R\\ = {\left( {4.124} \right)^2}\left( {0.400} \right)\\ = 6.{\rm{803 }}\frac{{\rm{m}}}{{{{\rm{s}}^{\rm{2}}}}}\end{aligned}\)

Obtain the tangential acceleration of a point on the rim of the disk at that instant is as follows:

\(\begin{aligned}{a_{\tan }} = {\alpha _z}R\\ = \left( {12.60} \right)\left( {0.400} \right)\\ = 5.{\rm{040 }}\frac{{\rm{m}}}{{{{\rm{s}}^{\rm{2}}}}}\end{aligned}\)

Determine the magnitude of the resultant linear acceleration of a point on the rim of the disk at that instant as follows:

\(\begin{aligned}a = \sqrt {{a_{Rad}}^2 + {a_{\tan }}^2} \\ = \sqrt {{{\left( {6.803} \right)}^2} + {{\left( {5.040} \right)}^2}} \\ = \sqrt {71.682402} \\ = 8.{\rm{467 }}\frac{{\rm{m}}}{{{{\rm{s}}^{\rm{2}}}}}\end{aligned}\)

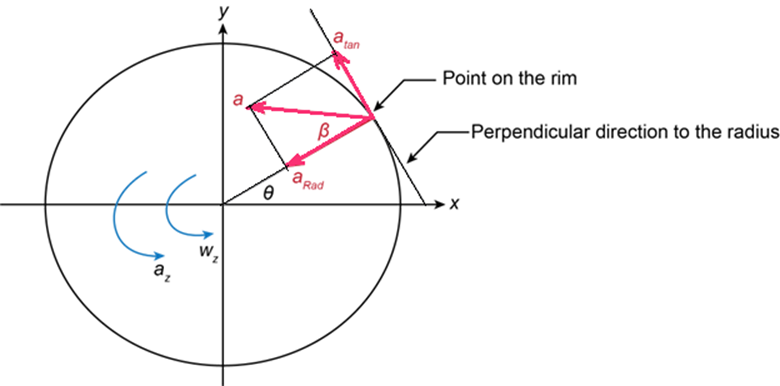
\(\begin{aligned}\beta = {\tan ^{ - 1}}\left( {\frac{{{a_{\tan }}}}{{{a_{Rad}}}}} \right)\\ = {\tan ^{ - 1}}\left( {\frac{{5.040}}{{6.803}}} \right)\\ = 36.5^\circ \end{aligned}\)

It is observed that \(0.10{\rm{0 rev}}\left( {\frac{{360^\circ }}{{1\,\,{\rm{rev}}}}} \right) = 36.0^\circ \) and that at \(t = 0 \to {\theta _0} = 0\,\,{\rm{rad}}\) \(\left( {{\mathop{\rm plug}\nolimits} \,\,\,t = 0{\mathop{\rm into}\nolimits} \,\,\theta \left( t \right)} \right)\).

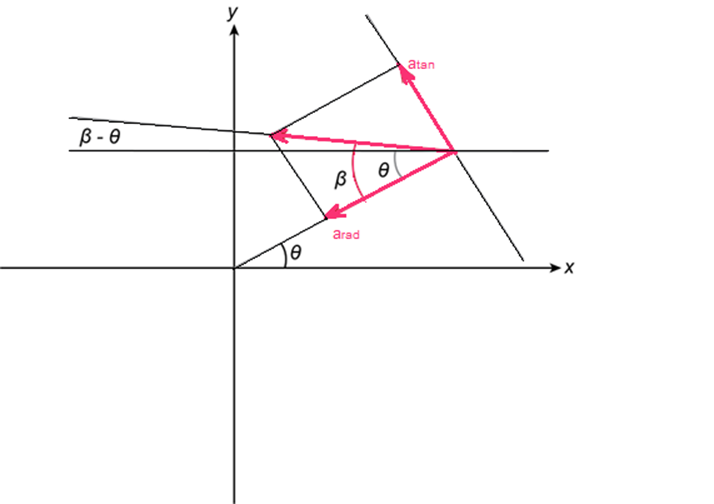
\(\begin{aligned}\beta - \theta = 36.5^\circ - 36.0^\circ \\ = 0.5^\circ \end{aligned}\)

Hence, the linear acceleration of the point of the rim if \(\theta = 0.1{\rm{00 rev}}\) would be \(8.{\rm{467 }}\frac{{\rm{m}}}{{{{\rm{s}}^{\rm{2}}}}}\) over the direction \(0.5^\circ \) from the negative x-axis.