A curve with a 120-m radius on a level road is banked at the correct angle for a speed of 20 m/s. If an automobile rounds this curve at 30 m/s, what is the minimum coefficient of static friction needed between tires and road to prevent skidding?

• The radius of the curve, $R=120m$.
• The designated speed of the road, $v=20m/s$.
• The speed of the automobile, $V=30m/s$.

According to Newton’s second law, the acceleration of the object is mainly dependent on the net force acting upon the object and the mass of the object. The equation of linear force is given by,

F = ma

Here, F is linear force, m is the mass of the object, a and is the acceleration of the object.

Draw the free-body diagram of the car when it moves on a level road banked at an angle$\theta$with a given speed v .

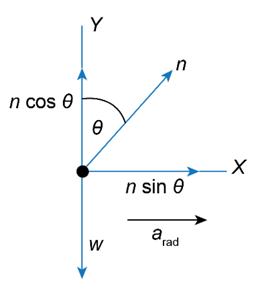
In the above diagram n represents the normal reaction, w represents the weight of the body,$a_{rad}$represents the radial acceleration, $n\sin \theta$represents the horizontal component of the normal reaction, and $n\cos \theta$the vertical component of the normal reaction.

The net force acting along the horizontal direction is given by,

$$\begin{gathered} n\sin \theta =\sum _{}{F}_x \\ n\sin \theta =m{a}_{rad} \\ n\sin \theta =\frac{m{v}^2}{R}.......\left(1\right) \end{gathered}$$

The net force acting along the vertical direction is given by,

$$\begin{gathered} \sum _{}{F}_y=0 \\ n\cos \theta -w=0 \\ n\cos \theta =w \\ n\cos \theta =mg.......\left(2\right) \end{gathered}$$

Divide equation (1) by (2), and we get,

$$\begin{gathered} \frac{n\sin \theta }{n\cos \theta }=\frac{{\displaystyle \frac{m{v}^2}{R}}}{mg} \\ \tan \theta =\frac{v^2}{gR} \end{gathered}$$

Substitute$20m/s$for v , $9.8m/s^2$for g , and 120 m for R in the above equation, and we get,

$$\begin{gathered} \tan \theta =\frac{{\left(20m/s\right)}^2}{\left(9.8m/s^2\right)\left(120m\right)} \\ \tan \theta =0.34 \\ \theta ={\tan }^{-1}\left(0.34\right) \\ =18.8° \end{gathered}$$

Draw the free-body diagram representing the case when frictional force arises.

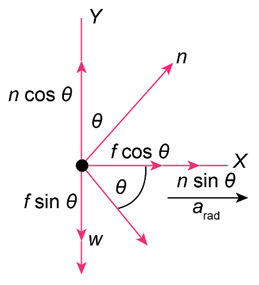
Let f be the frictional force.

The net force acting along the vertical direction is given by,

$n\cos \theta -f\sin \theta -w=0......\left(3\right)$

The net force acting along the horizontal direction is given by,

$f\cos \theta +n\sin \theta =m{a}_{rad}......\left(4\right)$

From the definition of frictional force,

$f={\mu }_{s\text{'}}n........\left(5\right)$

The radial acceleration is given by,

${\mathrm{a}}_{\mathrm{rad}}=\frac{{\mathrm{V}}^2}{\mathrm{R}}........\left(6\right)$

The weight is given by,

$w=mg.......\left(7\right)$

Substitute equation (5) and equation (6) in equation (4).

${\mu }_{s}n\cos \theta +n\sin \theta =m\frac{V^2}{R}........\left(8\right)$

Substitute equation (5) and equation (7) in equation (3).

$n\cos \theta -{\mu }_{s}n\sin \theta -mg=0......\left(9\right)$

Simplify equation (9) for .

$n=\frac{mg}{\cos \theta -{\mu }_s\sin \theta }......\left(10\right)$

Substitute equation (10) in equation (8).

$$\begin{gathered} {\mu }_s\frac{mg}{\cos \theta -{\mu }_s\sin \theta }\cos \theta +\frac{mg}{\cos \theta -{\mu }_s\sin \theta }\sin \theta =m\frac{V^2}{R} \\ {\mu }_s\frac{mg}{\cos \theta -{\mu }_s\sin \theta }\cos \theta +\frac{mg}{\cos \theta -{\mu }_s\sin \theta }\sin \theta =m\frac{V^2}{R} \\ {\mu }_{s}g\cos \theta +g\sin \theta =\frac{V^2}{R}\left(\cos \theta -{\mu }_s\sin \theta \right) \\ {\mu }_s=\frac{{\displaystyle \frac{V^2}{R}}\cos \theta -g\sin \theta }{g\cos \theta +\sin \theta {\displaystyle \frac{V^2}{R}}} \end{gathered}$$ ...........(11)

Substitute 30 m/s for V ,$9.8m/s^2$for g , 120 m for R , and$18.8°$for$\theta$in the equation (11), and we get,

$$\begin{gathered} {\mu }_s=\frac{{\displaystyle \frac{{\left(30m/s\right)}^2}{120m}}\cos \left(18.8°\right)-\left(9.8m/s^2\right)\sin \left(18.8°\right)}{\left(9.8m/s^2\right)\cos \left(18.8°\right)+\frac{{\left(30m/s\right)}^2}{120m}\sin \left(18.8°\right)} \\ =\frac{3.942}{11.694} \\ \approx 0.34 \end{gathered}$$

Therefore, the required static friction is 0.34 .